Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.6 - Ex. 77
Calcule o módulo da força trativa e o ângulo de forma que o olhal tenha uma força resultante de direcionada para baixo.
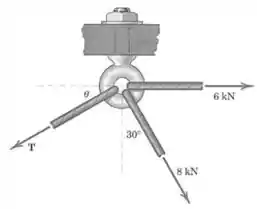
Passo 1
Nosso objetivo é gerar uma força resultante de módulo voltada inteiramente para baixo:
A primeira conclusão que podemos tirar disso é que as componentes horizontais das três forças têm que se cancelar perfeitamente:
E as forças na direção vertical têm que somar exatamente :
E então ficamos com o seguinte sistema:
Passo 2
Vamos resolver esse sistema para encontrar . Se dividirmos a segunda equação pela primeira:
Agora podemos substituir isso em qualuqer uma das equações do sistema para encontrar o módulo :
Resposta
O ângulo é e a tração é .
Exercícios de Livros Relacionados
Três forças de uma mesma intensidade P atuam no cubo de lado a como mostrado na figura. Substiua as três forças por um torsor equivalente e determine a a intensidade, a direção e o sentido da resultan
Um grupo de estudantes carrega um reboque de 2 × 3,3m com duas caixas de 0,66 × 0,66 × 0,66m e uma caixa de 0,66 × 0,66 × 1,2m . Cada caixa est[a colocada na traseira do reboque e alinhada pelos seus
Um momento de 4N ⋅ m é aplicado ao cabo da chave de fenda. Decomponha esse momento de binário em um par de forças de binário F exercidas sobre o cabo e P exercidas sobre a ponta da chave.
As extremidades da placa triangular estão sujeitas a três binários. Determine a intensidade da força F de modo que o momento de binário resultante seja 400N ⋅ m em sentido horário.
Se θ = 30 ° , determine a intensidade da força F de modo que o momento de binário resultante seja 100N ⋅ m , em sentido horário. O disco tem um raio de 300m m .