Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 68
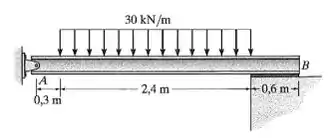
Determine a tensão de flexão máxima absoluta na viga. A seção transversal é retangular com
base de e altura .
Passo 1
Fala aí pessoal, partiu mais um problema de resmat. Ele pediu a tensão de flexão máxima absoluta nesse cara. Então a gente precisa achar nele o momento máximo e usar a fórmulinha da flexão para a tensão. Bora!
Primeiramente, a gente vai começar observando as propriedades geométricas dessa seção.
Vamos começar pelo momento de inérciaele será dado por:
É isso. Vamos seguir!
Passo 2
Aí a gente quer o momento máximo nessa viga. Precisamos do diagrama de momento. A
Primeiro se acha as reações de apoio:
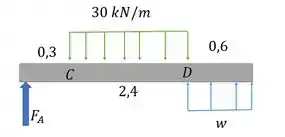
Podemos calcular e pelas equações de equilíbrio:
Passo 3
Depois as equações para o momento.
Seção AC:
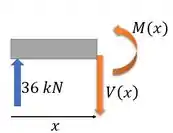
Aí a gente esquece o resto da viga à direita, e foca só nessa parte. Fica assim:
Seção CD:
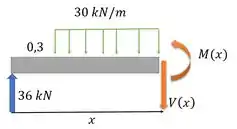
E o somatório de momentos em relação a extremidade direita desse desenhinho:
Seção DB:
Passo 4
As equações são:
Às vezes as equações ficam feias, mas para esboçar, você pode achar alguns pontos chave (onde as curvas cortam os eixos coordenados e nos extremos das seções), os valores máximos e mínimos, e se ligar no tipo de curva que precisa fazer.
Utilizando as equações podemos traçar o gráfico
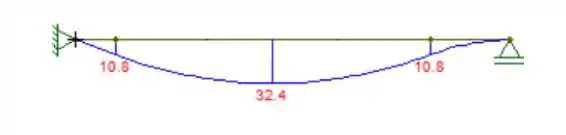
Aqui nós usamos a conveção do momento positivo na parte de baixo.
Passo 5
Temos tudo agora para montar a fórmulinha da tensão:
Podemos ver que o momento máximo vale 32,4kNm. é o momento de inércia calculado. Quem é ?
Cara, ele é a distância do eixo horizontal que passa pelo centroide até o ponto onde nossa tensão é calculada. A tensão vai ser máxima nas extremidades da peça mais longes desse eixo.
Sendo assim, como nossa peça é simétrica, a tensão nas extremidades vão ter valores numéricos iguais e nosso vale: