Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 34
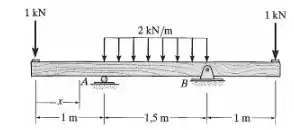
Represente graficamente os diagramas de força cortante e momento fletor para a viga de madeira e determine a força cortante e o momento fletor em todo o comprimento da viga em função de .
Passo 1
Primeiramente, vamos calcular as reações de apoio utilizando as equações de equilíbrio:
Passo 2
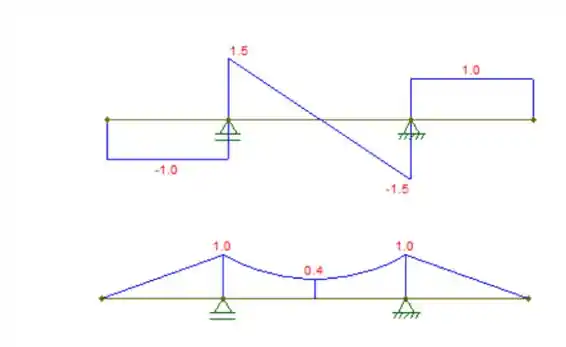
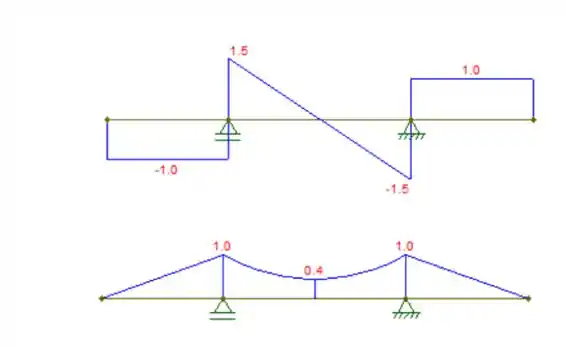
Com as reações calculadas, podemos fazer os diagramas de cortante e momento fletor, respectivamente:
Passo 3
O problema nos pede as expressões do cortante e momento para toda a viga. Para isso, devemos separar a viga em trechos e caminhar pela viga com uma distância arbitrária x e adicionar os esforços existentes nesta:
No primeiro trecho
No segundo trecho
No terceiro trecho
Repare que as forças passam invertidas de um trecho para outro, como se houvesse uma rótula.
Resposta
No primeiro trecho
No segundo trecho
No terceiro trecho
