Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 79

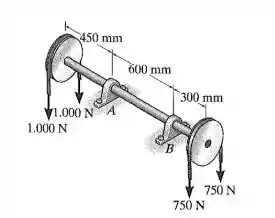
Se o eixo tiver diâmetro de 37,5   m m , determine a tensão de flexão máxima absoluta no eixo.

Passo 1

Falaaa! Se a gente quer a tensão máxima, precisamos da flexão máxima.

Vamos, primeiramente, determinar as reações:

∑ M a = 0 → 2000 × 0,45 + 0,6 F b - 1500 × 0,9 = 0

F b = 750 N

∑ F y = 0 → F a + 750 - 2000 - 1500 = 0

F a = 2750 N

Passo 2

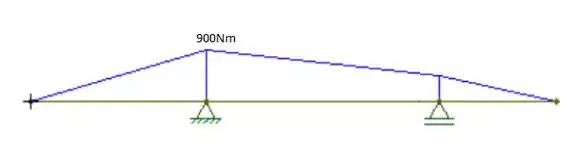
Com essas reações, conseguimos achar o diagrama do momento. Como a gente só tem cargas pontuais, o diagrama vai ser linear.

Se vai ser linear, é mais tranquilo a gente achar o momento nos pontos chave (pontos de aplicação da força e extremidades) e depois só ligar eles por retas.

O momento nas extremidades é zero, porque nelas a gente não tem momento concentrado ou reação de momento.

Vamos analisar os pontos A e B . A gente corta a barra neles e oha só para um lado. Os momentos são achados pelos equações de equilíbrio. (lembra de colocar o momento na convenção positiva).

Para o ponto A teremos:

∑ M A = 0 → M + 2000 ⋅ 0,45 = 0 ∴ M = - 900   N ⋅ m

Para o ponto B teremos:

∑ M B = 0 → M + 2000 ⋅ 1,05 - F a ⋅ 0,6 = 0 ∴ M = - 450   N ⋅ m

Fazendo o diagrama de momento:

Passo 3

Podemos ver que M m á x = 900 N m . Logo, a gente usa a fórmula da tensão para achar a tensão máxima:

σ m a x = M c I

Para ser a tensão máxima em relação a seção, c deve ser a maior distância do eixo do momento até a borda da seção, ou seja, metade do diâmetro:

c = 37,5 2   m m

O momento de inércia é dado por:

I = r 4 π 4 = π 4 × 0,01875 4   m 4

Nossa tensão fica:

σ m á x = 900 × 0,01875 π 4 × 0,01875 4 = 173,84 M P a

Resposta

σ m á x = 173,84 M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga e carregamento do P r o b. 4.30 , determinar:A variação da largura da borda superior AB da aba;A variação do comprimento da linha de centro DE.
Foi assumido na SEC.4.4 , que as tensões normais σ y em um membro em flexão pura são desprezadas. Para um membro elástico, de seção transversal retangular, inicialmente reto, pede-se:Derivar uma expre
Duas barras de latão são unidas firmemente a duas barras de alumínio, formando a seção composta mostrada. Usando os dados abaixo, determinar o maior momento fletor permissível, quando a viga é encurva
Um perfil laminado de aço W 410 x 114 está sujeito a um momento M de 360k N m . Sabendo-se que E = 200G P a e ϑ = 0,30 , determinar:A variação da largura da aba superior;A variação do comprimento da m
Para a barra do Prob. 4.102, determine: (a) a máxima tensão, quando o raio de curvatura da barra for 4 m; (b) o correspondente valor do momento fletor. (Veja sugestão dada no Prob. 4.102.)