Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 43
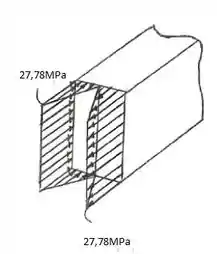
Um elemento com as dimensões mostradas na figura deverá ser usado para resistir a um momento fletor interno M = 2 kN.m. Determine a tensão máxima no elemento se o momento for aplicado (a) em torno do eixo z e (b) em torno do eixo y. Trace um rascunho da distribuição de tensão para cada caso.
Passo 1
Fala galerinha do RespondeAí, tudo bem com vocês?
Saca só, nesse exercício aqui o enunciado nos diz que um elemento com as dimensões mostradas na figura deverá ser usado parar resistir a um momento fletor interno dado como . Sabendo disso, na letra (a) ele nos pede pra determinar a tensão máxima no elemento se o momento for aplicado em torno do eixo .
- Primeiramente, sabemos que a fórmula para tensão na flexão é:
Onde c é a distância até a linha neutra em relação a cada eixo (no caso do problema ela deve ser máxima para a tensão ser máxima).
Como a letra a nos pede o efeito do momento em torno de z:
-6
Segue que:
6
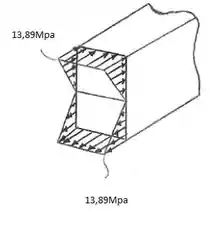
Representando a distribuição da tensão:
Passo 2
b) Novamente, vamos utilizar a fórmula:
Só que agora a rotação é em torno e y:
-6
6
Representando a distribuição da tensão:
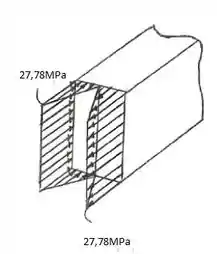
Resposta
b)
