Enunciado
Mecânica e Resistência dos Materiais - Dinamica Classica de Particulas e Sistemas - Marion- Ed: 5º - Capítulo 1.Problemas - Ex. 38
Determine o valor da integral , se o vetor A = yi + zj + xk e S é a superfície definida pelo parabolóide z = 1 – x2 – y2, onde z 0.
Passo 1
E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de matrizes, vetores e cálculo vetorial.
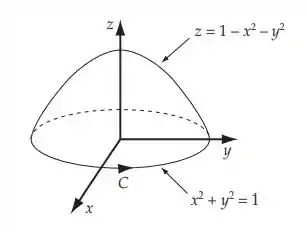
Pelo teorema de Stoke, temos:
A curva C que envolve nossa superfície S é o círculo unitário que se encontra no plano xy. Como o elemento de área na superfície da é escolhido para fora da origem, a curva é direcionada no sentido anti-horário, conforme exigido pela regra da mão direita. Agora mudando para coordenadas polares, de modo que tenhamos:
E como:
Temos que:
Resposta
Ver passo a passo.
Exercícios de Livros Relacionados
Determine a intensidade e a direção θ de F A de modo que a força resultante seja direcionada ao longo do eixo x positivo e tenha uma intensidade de 1250N .
Se a força resultante dos dois rebocadores tiver de ser direcionada para o eixo x positivo, e F B tiver a mínima intensidade, determine as intensidades de F ReF B e o ângulo θ .Fonte: Estática Mecânic
Determine os ângulos feitos pelo vetor V = 40 i - 30 j com o eixo positivo dos x e dos y . Escreva o vetor unitário n na direção de V .
Qual é a massa, tanto em slugs quanto em quilogramas, de um carro com 3000l b ?
Determine o peso, em newtons, de uma mulher cujo peso é de 130l i b r a s . Ache, também, sua massa em slugs e em quilogramas. Determine seu próprio peso em newtons.