Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 2.Problemas - Ex. 27
Se a força resultante dos dois rebocadores tiver de ser direcionada para o eixo x positivo, e tiver a mínima intensidade, determine as intensidades de e o ângulo .
Fonte: Estática Mecânica para Engenharia – 14ª ed
Passo 1
E aí galerix, tudo de boas até aqui?!
Vai dar certo!
Bem, a respeito de decomposição de forças, mais uma vez vamos lembrar, até abusar, sempre das 3 coisas para a melhor resolução de problemas envolvendo força resultante:
- Regra do paralelogramo;
- Lei dos senos;
- Lei dos cossenos.
E lembrando que, nesse capítulo, serão de suma importância a aplicação dessas 3 leis e regras.
Agora nosso problema quer realmente a força resultante, e temos que analisar um pouco mais detalhadamente.
Bora lá!!
Passo 2
Bem, a gente sabe como encontrar o , não sabe?
Primeiro com nosso esboço:
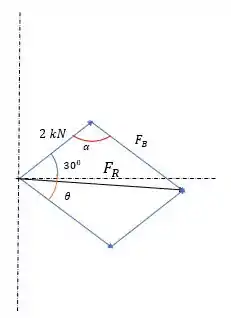
Bem, fazendo a velha amiga a Lei dos Cossenos, para encontrar o valor de , fica:
Pronto. O problema pede que seja o menor possível, isso implica também que será o menor possível.
Para o ser o menor possível, o valor de deveria ser o maior possível, concordamos?
Pois bem, o maior valor possível de é igual a 1, e para isso ele deveria ser zero, o que sabemos que não é possível, pois ele é, no mínimo , devido ao ângulo de que o problema dá.
Se analisarmos o esboço, podemos perceber que o ângulo deve ser o menor possível para que seja o maior possível. E para que seja pequeno, a soma deve ser grande.
Aí matamos a charada, qual o maior valor positivo que pode ser??
Exato, .
Então
Passo 3
O novo esboço fica:
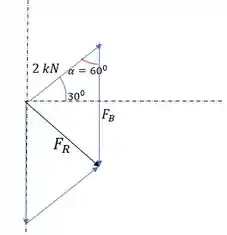
Se , então . Assim a eq. 1 fica:
A mínima intensidade que pode assumir é de 1 kN;
Assim, temos:
Resposta
Portanto: