Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 1.Problemas - Ex. 1
Determine os ângulos feitos pelo vetor com o eixo positivo dos e dos . Escreva o vetor unitário na direção de .
Passo 1
Olá, tudo bem com você?
Vamos iniciar esse problema ilustrando o vetor em questão. O problema pede que determinemos os ângulos que ele forma com o eixo positivo dos e dos .
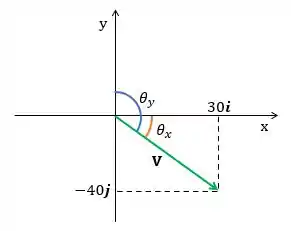
Passo 2
O próximo passo é calcular o módulo do vetor :
Em posse do módulo, encontramos os ângulos:
E
Passo 3
O vetor unitário n é um vetor cuja magnitude vale um e cuja direção coincide com a do vetor V. Sabemos que o vetor V pode ser representado por
Então,
Resposta
Exercícios de Livros Relacionados
2.19. A caminhonete precisa ser rebocada usando duas cordas. Se a força resultante deve ser de 950N , orientada ao longo do eixo x positivo, determine as intensidades das forças F AeF B Que atuam sobr
2.14. Determine o ângulo θ ( 0 ° ≤ θ ≤ 90 ° ) para o tirante AB, de modo que a força horizontal de 800N tenha uma componente de 1000N direcionado de A até C. Qual é a componente da força que atua ao l
2.20. Se Φ = 45 ° , F 1 = 5k N e a força resultante é de 6k N , orientada ao longo do eixo y positivo, determine a intensidade necessária de F 2 e sua direção θ.
2.15. Determine o ângulo Φ ( 0 ° ≤ Φ ≤ 90 ° ) entre os tirante AB e AC, de modo que a força horizontal de 800N tenha uma componente de 1200N que atue para a esquerda, na direção de B para A. Considere
2.15. Decomponha F 2 nas componentes que atuam ao longo dos eixos u ev e determine suas intensidades.