Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 7

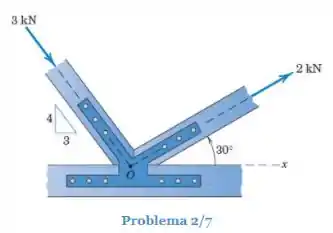
Os dois elementos estruturais, um sob tração e o outro sob compressão, exercem as forças indicadas no nó O . Determine o módulo da resultante R das duas forças e o ângulo θ que R faz com o eixo x positivo.

Passo 1

Olá, tudo bem com você?

Vamos começar analisando o problema. Queremos determinar o módulo da resultante R das duas forças e o ângulo θ que R faz com o eixo x positivo. Observe que não temos o ângulo que F = 3   k N faz com o eixo x negativo, mas temos um triângulo no qual podemos fazer uma relação. Chamaremos esse ângulo de γ :

γ = tan - 1 ⁡ 4 3

γ = 53,1 °

Esse valor já foi representado no gráfico abaixo.

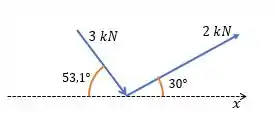
Para encontrar as componentes da resultante em x e em y , faremos o somatório das forças.

Em x :

R x = ∑ F x = 3 cos ⁡ 53,1 ° + 2 cos ⁡ 30 °

R x = 3,53   k N

Observe que ambas as forças estão no sentido positivo de x .

Em y :

R y = ∑ F y = - 3   s e n   53,1 ° + 2   s e n   30 °

R y = - 1,4 °   k N

Veja que uma das forças está no sentido negativo de y .

Passo 2

Encontramos as componentes, agora podemos calcular o módulo da resultante R .

R 2 = R x 2 + R y 2

R 2 = 3,53 2 + - 1,4 2

R = 3,8   k N

Passo 3

E o ângulo θ que R faz com o eixo x positivo é:

θ = tan - 1 ⁡ R y R x

θ = tan - 1 ⁡ - 1,4 3,53

θ = - 21,6 °

Quando o ângulo dá negativo, corresponde ao giro no sentido horário. Então, para encontrar o ângulo positivo correspondente fazemos,

θ = 360 ° - 21,6 °

θ = 338,4 °

Ambas as respostas são corretas!

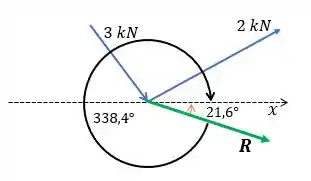
Resposta

R = 3,8   k N

θ = 338 , 4 °

ou

θ = - 21,6 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine as interseções xey da linha de ação da resultante dos três carregamentos aplicados ao conjunto de engrenagens.
A viga de aço em balanço, com flanges e suportes rebitados, é submetida ao binário das duas forças mostradas e seus efeitos sobre a ligação em A devem ser determinados. Substitua as duas forças e o bi
O comprimento não esticado da mola é b . Determinar a força que a mola exerce sobre o ponto B da armação se b=0,3m . O módulo da força da mola é a constante da mola k multiplicado pela deflexão (por a
A treliça do tipo telhado assimétrico é usada quando é desejável, para fins de energia solar, um ângulo normal de incidência da luz solar sobre a superfície virada para o sul A B C . Os cinco carregam
Substitua as três forças que atuam na haste dobrada por um sistema força-binário equivalente no ponto A do suporte. Em seguida, determine a interseção x da linha de ação da força resultante independen