Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 45
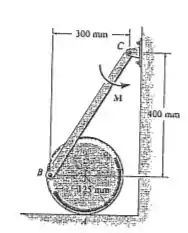
O disco de se apoia sobre a superfície para a qual o coeficiente de atrito estático Determine o maior momento de binário que pode ser aplicado à barra sem causar movimento.
Passo 1
Desejamos encontrar o valor do maior momento de binário aplicável de tal forma que não venha causar movimento. Para isso, tomemos o seguinte diagrama de forças
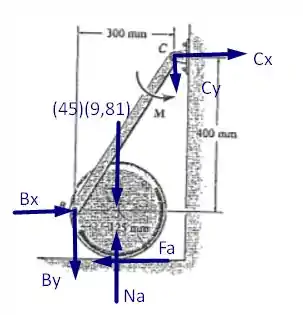
Tomemos, agora, as equações de equilíbrio para encontrarmos o que desejamos. Dessa forma, teremos
Resolvendo o sistema composto por essas equações vamos obter
Por fim, vamos calcular o momento no ponto para encontrarmos a medida que desejamos
Resposta
Exercícios de Livros Relacionados
O cilindro de 20k g A e o cilindro de 50k g B estão ligados por meio de uma corda que passa emtorno de um pino áspero por duas voltas e meia. Se os cilindros estão na iminência de movimento, determine
O veículo, que tem massa de 3,4M g , deve descer a rampa com velocidade constante, sendo para isso sustentado pela corda enrolada na árvore e mantida esticada pelo homem. Se as rodas estão livres para
Se uma força P = 30N for aplicada ao cabo da alavanca, determine o maior momento de binário M que pode ser resistido de modo que a roda não gire. O coeficiente de atrito estático entre a correia e a r
Mostre que a relação de atrito entre as trações na correia, o coeficiente de atrito m e os contatos angulares α e β para a correia em “ V ” é T 2 = T 1 e μ β / sen ( α / 2 ) .
Um cabo é preso à placa B de 20k g , passa por um pino fixo em C e é preso ao bloco em A .Usando os coeficientes de atrito estático mostrados, determine a menor massa do bloco A que impeça o movimento