Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 11.Problemas - Ex. 52
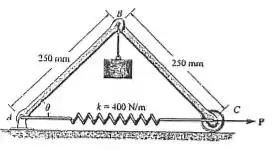
As ligações uniformes e pesam cada uma e o cilindro pesa . Determine a força horizontal necessária para manter o mecanismo em A mola tem um comprimento livre de .
Passo 1
Desejamos determinar o valor da força horizontal para manter o mecanismo sob o ângulo descrito. Vemos que o sistema possui apenas um grau de liberdade definido pela coordenada independente . Com o deslocamento virtual vamos denominar as posições dos pontos por . Assim
Passo 2
Tomando vamos ter
Substituindo as equações do passo anterior vamos chegar em
Dado que e usando vamos obter
Resposta
Exercícios de Livros Relacionados
A haste uniforme A B tem massa de 5k g . Se a mola conectada não está deformada quando θ = 90 ° , determine o ângulo θ de equilíbrio usando o método do trabalho virtual. Observe que a mola sempre perm
Os elementos uniformes A B e B C possuem massa de 1k g cada e o cilindro possui 10k g . Determine a força horizontal P necessária para manter o mecanismo em posição quando θ = 45 ° . A mola tem compri
Para o mecanismo mostrado, a mola de rigidez k tem um comprimento não alongado de essencialmente zero, e o elo maior tem uma massa m com centro de massa em B. A massa do elo menor é desprezível. Deter
Duas barras idênticas são soldadas em um ângulo de 120∘ e articuladas em O conforme mostrado. A massa da aba de suporte é pequena em comparação com a massa das barras. Investigue a estabilidade da pos
A alça é presa a uma das engrenagens conectadas por mola, que são montadas em rolamentos fixos. A mola de rigidez k conecta dois pinos montados nas faces das engrenagens. Quando a alça está na posição