Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.9 - Ex. 211
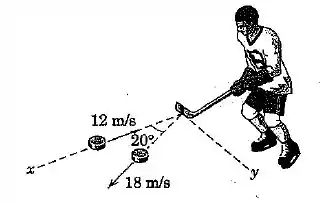
O disco de hóquei no gelo com uma massa de tem uma velocidade de antes de ser atingido pelo taco de hóquei. Após o impacto o disco se desloca na nova direção mostrada com uma velocidade de . Se o taco está em contato com o disco por , calcule o módulo da força média exercida pelo taco sobre o disco durante o contato, e encontre o ângulo feito por com a direção .
Passo 1
A chave para essa questão é considerar a conservação de momento linear em cada uma das direções separadamente. Vamos começar com a direção , qual é a componente da velocidade inicial nessa direção?
E qual a componente da velocidade final nessa direção?
Como o disco de hóquei tem massa e a colisão dura , podemos usar o teorema do impulso para calcular a média da força feita pelo taco na direção :
Passo 2
Agora vamos fazer praticamente a mesma coisa com a direção . A velocidade inicial é:
(Atenção para o sinal!) E a velocidade final em é:
Agora vamos aplicar o mesmo teorema de antes:
Passo 3
Isso quer dizer que o módulo da força média é:
Agora falta calcular o ângulo entre e a direção . Como já temos as duas componentes do vetor, podemos usar a fórmula de sempre:
Resposta
O módulo da força média é e o ângulo é .