Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 17.Problemas - Ex. 86

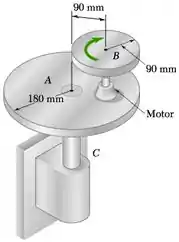
O disco B de 4 kg está ligado ao eixo de um motor montado sobre a placa A, que pode girar livremente em torno do eixo vertical C. A unidade motor-placa-eixo tem um momento de inércia de 0,20 kg ∙ m2 em relação à linha de centro do eixo C. Se o motor é ligado quando o sistema está em repouso, determine as velocidades angulares do disco e da placa após o motor ter atingido sua velocidade normal de operação de 360 rpm.

Passo 1

O enunciado pede que a gente determine as velocidades angulares do disco e da placa após o motor ter atingido sua velocidade normal de operação de 360 rpm.

Momentos de inércia. eixo da placa do motor:

I C = 0.20   kg ∙ m 2

Disco:

I B = 1 2 m B r B 2 = 1 2 4   kg 0.090   m 2 = 0.0162   kg ∙ m 2

Passo 2

Cinemática.

v B = r B / C ω C = 0.090 ω C

Momentos sobre C:

I C ω C + m B r B / C ω C r B / C - I B ω B = 0

I C + m B r B / C 2 ω C = I B ω B

0.20 + 4 0.090 2 ω C = 0.0162 ω B

ω C = 0.069707

Passo 3

Velocidade angular do motor.

ω M = ω B + ω C = 1.06971 ω B

ω M = 360   rpm

ω B = ω M 1.06971 = 360   rpm 1.06971 = 336.54   rpm

ω C = 0.069707 336.54   rpm

Resposta

ω B = 337   rpm

ω C = 32.5   rpm

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois discos de mesma espessura e mesmo material são presos a um eixo como mostrado na figura. O disco A de 4 kg tem um raio rA 100 mm e o disco B tem um raio r B 150 mm. Sabendo que o binário M de int
Mostre que a soma H A dos momentos sobre um Ponto A dos momentos das partículas de uma laje rígida em movimento plano é igual a I A ω , onde ω é a velocidade angular da laje no instante considerado e
O disco A de 7,5 lb tem raio rA = 6 pol. E está inicialmente em repouso. O disco B de 10 lb tem um raio = 8 pol. e uma velocidade angular ω 0 de 900 rpm quando ele é colocado em contato com o disco A.
Mostre que o sistema de momentos para uma laje rígida em movimento plano se reduz a um único vetor, e expresse a distância do centro de massa G à linha de ação desse vetor em termos do centroide raio
Um disco de espessura uniforme, inicialmente em estado de repouso, é posto em contato com uma esteira que se move com velocidade constante v. Representando por k o coeficiente de atrito cinético entre