Exercícios de Impulso e Quantidade de Movimento Angular - Lista de Exercícios Resolvida
Questão 1
As pequenas esferas, que possuem as massas e velocidades iniciais indicadas na figura, atingem e tornam-se presas às extremidades pontudas da haste, que é livremente articulada em e está inicialmente em repouso. Determine a velocidade angular do conjunto após o impacto. Despreze a massa da haste.
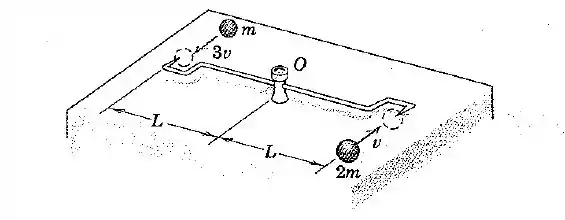
Questão 2
O conjunto parte do repouso e atinge uma velocidade angular de , sob a ação de uma força de aplicada à corda por segundos. Determine . Despreze o atrito e todas as massas exceto a das quatro esferas de , que podem ser tratadas como partículas.
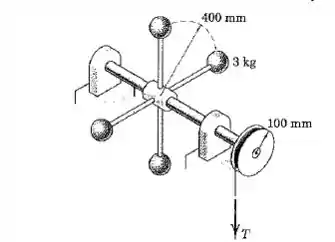
Questão 3
Em um dado instante, a partícula de massa tem a posição e velocidade mostradas na figura, e sofre a ação da força . Determine sua quantidade de movimento angular em torno do ponto e a taxa de variação no tempo dessa quantidade de movimento angular.
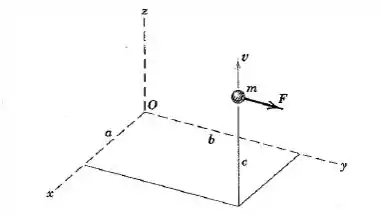
Questão 4
Uma partícula de massa se desloca com atrito desprezível sobre uma superfície horizontal e está conectada a uma mola leve presa em . Na posição a partícula tem a velocidade = 4 m/s. Determine a velocidade da partícula quando ela passa a posição .
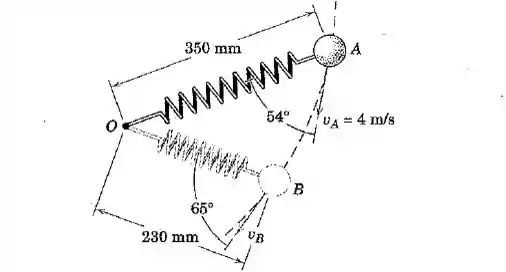
Questão 5
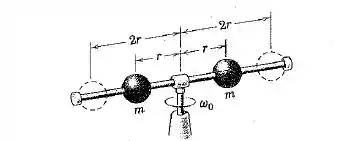
As duas esferas de massas iguais podem deslizar ao longo da haste horizontal que gira. Se elas estão iniciamente travadas na posição a uma distância do eixo de rotação com o conjunto girando livremente com uma velocidade angular , determine a nova velocidade angular após as esferas serem liberadas e finalmente assumirem posições nas extremidades da haste na distância radial de . Encontre também a fração da energia cinética inicial do sistema que é perdida. Despreze a pequena massa da haste e do eixo.
Questão 6
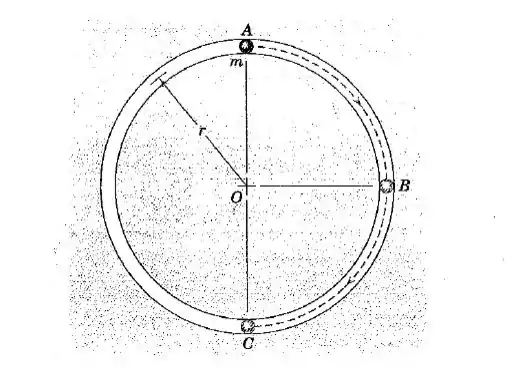
A partícula de massa é suavemente empurrada a partir da posição de equilíbrio e posteriormente desliza ao longo da trajetória circular lisa que se situa num plano vertical. Determine o módulo da sua quantidade de movimento angular em torno do ponto quando ela passa (a) o ponto e (b) o ponto . Em cada caso, determine a taxa de variação no tempo de .
.
Questão 7
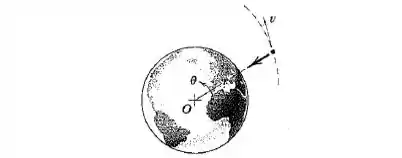
A única força atuando sobre um satélite da Terra que se desloca fora da atmosfera terreste é a atração gravitacional radial. O momento desta força é nulo em torno do centro da Terra tomado como um ponto fixo. Prove que permanece constante durante o movimento do satélite.
Questão 8
03) A figura mostra uma barra delgada AB de comprimento e massa articulada a um disco de raio e massa este último apoiado sobre uma pista horizontal áspera. O sistema parte do repouso sujeito a uma força horizontal aplicada ao centro A do disco. Sabendo que o disco rola sem escorregar, pede-se, para o instante da partida (instante imediatamente após a aplicação da força ):
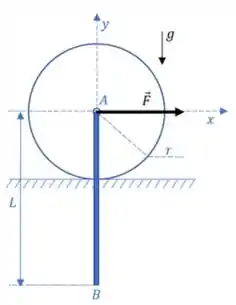
a) Desenhar os diagramas de corpo livre do disco e da barra.
b) Escrever as equações do teorema da resultante e do teorema do momento da quantidade de movimento para o disco e para a barra.
c) Escrever as equações da cinemática pertinentes.
d) Determinar as acelerações angulares do disco e da barra.
Ver solução completaQuestão 9
01) Um carretel de massa , de centro e raios (externo) e (interno) está articulado a uma barra de massa e comprimento , conforme indicado na figura. Mediante a aplicação de uma força (constante) a um cabo inextensível e de massa desprezível enrolado ao carretel, faz-se com que este role sem deslizar sobre um plano horizontal, arrastando consigo a barra . A polia de centro tem massa desprezível e o coeficiente de atrito entre as superfícies da barra e do plano horizontal é . é o ponto de contato do carretel com o plano horizontal. O momento de inércia do carretel em relação ao eixo é dado: . Pede-se:
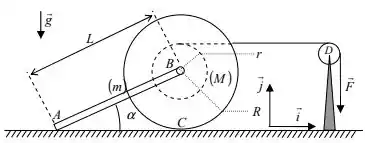
a) desenhar os diagramas de corpo livre do carretel e da barra;
b) determinar o momento de inércia do carretel em relação ao eixo ;
c) expressar as acelerações do baricentro da barra e do baricentro do carretel em função da aceleração angular do carretel;
d) escrever as equações dos teoremas do movimento do baricentro (TMB) e do momento da quantidade de movimento (TMQM ou TQMA, se se utilizar a terminologia ‘Teorema da Quantidade de Movimento Angular) para o carretel e para a barra.
Ver solução completaQuestão 10
02) No mecanismo da figura ao lado, um disco de raio , articulado em seu centro a uma barra de comprimento rola sem escorregar sobre um plano horizontal fixo. A extremidade da barra está articulada a um bloco que desliza sobre uma guia vertical com velocidade constante. Para o instante considerado na figura, pede-se:
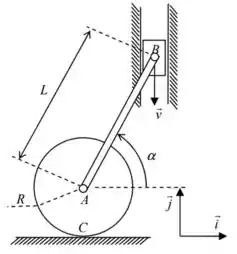
a) o CIR da barra
b) a velocidade angular da barra
c) a velocidade do ponto
d) a velocidade angular do disco;
e) a aceleração angular da barra ;
f) a aceleração do ponto ;
Ver solução completaQuestão 11
02) Conforme mostrado na figura, a barra se move no plano mantendo contato permanente com a semicircunferência de centro e raio e com o eixo horizontal . Admita-se, ainda, que a extremidade da barra se mova com velocidade ( constante). Expressando os resultados na base ligada à barra, determine para o instante em que :
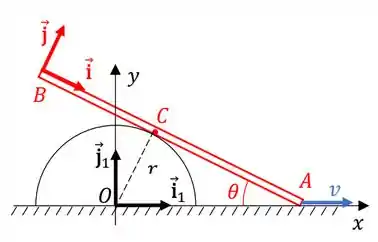
a) As componentes segundo as direções (nesta ordem) da velocidade do ponto de contato barra.
b) A velocidade angular da barra .
c) A aceleração angular da barra
d) As componentes nas direções (nesta ordem) da aceleração do ponto barra.
Ver solução completaQuestão 12
03) No sistema mostrado na figura a barra , de massa e comprimento , está articulada no ponto ao disco de massa e raio . O sistema está inicialmente em repouso, com a barra na posição vertical e com a reta que passa por e inclinada em um ângulo em relação à horizontal. Para o instante imediatamente após a liberação do sistema, determine:
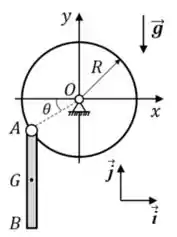
a) O vetor aceleração angular da barra.
b) A aceleração do centro de massa da barra.
c) O vetor aceleração angular do disco.
d) A força que a barra aplica no disco pela articulação do ponto .
Ver solução completa