Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 43

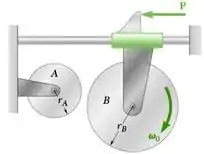
O disco A de 3 kg tem raio rA = 75 mm e velocidade angular inicial ω 0 = 375 rpm no sentido horário. O disco B de 7,5 kg tem um raio rB = 125 mm e está em repouso. Uma força P de 12,5 N de intensidade é então aplicada para pôr os discos em contato. Sabendo que μ s = 0,25 entre os discos e desprezando o atrito do mancal, determine (a) a aceleração angular de cada disco, (b) a velocidade angular final de cada disco.

Passo 1

Enquanto o escorregamento ocorre:

F = μ k N = μ k P = 0 , 25 12,5   N = 3,125   N

Disco A:

+ Σ M A = Σ M A eff :             F r A = I - A α = 1 2 m A r A 2 α A

F = 1 2 m A r A α

3,125   N = 1 2 3   k g 0,075   m α A

α A = 27,78   r a d / s 2

Passo 2

Disco B:

+ Σ M B = Σ M B eff :             F r B = I - B α B = 1 2 m B r B 2 α B

F = 1 2 m B r B α

3,125   N = 1 2 7,5   k g 0,125   m α B

α B = 6,67   r a d / s 2  

Passo 3

  1. Velocidades angulares finais.

ω A 0 = 375   rpm 2 π 60 = 39 , 27   rad/s  

ω B 0 = 0

Quando os discos param de deslizar

v P = v P :             ω A γ A = ω B γ B

ω A 0 - α A t γ A = α B t γ B

39 , 27 - 27,78 t 0,075   m = 6 , 67 t 0,150

t = 0,955   s  

ω A = ω A 0 - α A t = 39 , 27 - 27,68 0,955

ω A = 12,84   rad/s 60 2 π

ω A = 122,61   r p m

Passo 4

Eq. (1)

12,84   rad/s 60 2 π 0,075   m = ω B 0,150   m

ω B = 61,31   r p m

Resposta

α A = 27,78   r a d / s 2

α B = 6,67   r a d / s 2

ω A = 122,61   r p m  

ω B = 61,31   r p m  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o Problema 16.27, considerando que a direção do movimento da correia é revertida.PROBLEMA 16.28 Um disco de raio 180 mm está em repouso quando é colocado em contato com uma correia em moviment
O tambor de freio de 200 mm de raio é unido a um volante maior que não está mostrado na figura. O momento de inércia total da massa do tambor e do volante é de 20 kg ∙ m2 e o coeficiente de atrito cin
Cada uma das roldanas duplas mostradas na figura tem um momento de inércia de massa de 20 ∙ kg m2 e está inicialmente em repouso. O raio externo é de 500 mm e o interno de 250 mm. Determine (a) a acel
O volante de motor mostrado na figura tem um raio de 500 mm, massa de 120 kg e um raio de giração de 375 mm. Um bloco A de 15 kg é preso a um fio que é enrolado em torno do volante e o sistema é solto
Resolva o Problema 16.30, considerando que velocidade angular inicial do volante é de 360 rpm no sentido horário.PROBLEMA 16.30 O tambor de freio de 200 mm de raio é unido a um volante maior que não e