Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 28

Resolva o Problema 16.27, considerando que a direção do movimento da correia é revertida.

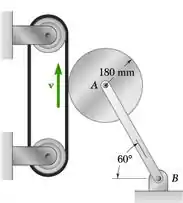
PROBLEMA 16.28 Um disco de raio 180 mm está em repouso quando é colocado em contato com uma correia em movimento com velocidade constante. Desprezando o peso da haste de conexão AB e sabendo que o coeficiente de atrito cinético entre o disco e a correia é 0,40, determine a aceleração angular do disco enquanto ocorre o deslizamento.

Passo 1

E ai galera tudo certinho? O enunciado pede que a gente determine a aceleração angular do disco enquanto ocorre o deslizamento, vamos dividir em cinto e disco, partiu :D

Cinto:

F = μ k N

Disco:

→ + Σ F x = Σ F x eff :             N - F A B cos ⁡ θ ;                 F A B cos ⁡ θ = N

+ ↑ Σ F y = Σ F y eff :             F A B sin ⁡ θ - m g - μ k N = 0

F A B sin ⁡ θ = m g + μ k N

Passo 2

Equalizando as equações temos:

Eq. (2) Eq. (1) :             tan ⁡ θ = m g - μ k N N

N tan ⁡ θ = m g + μ k N ;               N = m g tan ⁡ θ - μ k

+ Σ M A = Σ M A eff :               F r = I - α

Passo 3

Para determinarmos a aceleração temos:

α = F r r = μ k N r I = μ k r 1 2 m r 2 ∙ m g tan ⁡ θ - μ k = 2 g r ∙ μ k tan ⁡ θ - μ k

Dados:

r = 0.18   m,       θ = 60 ° ,               μ k = 0.40

α = 2 9.81   m/ s 2 0.18   m ∙ 0.40 tan ⁡ 60 ° - 0.40

Resposta

α = 32.7   rad/ s 2  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma placa retangular uniforme tem massa de 5 k g e é mantida na posição por três cordas mostrado na figura. Determine o maior valor de θ para que ambas nas cordas AD e BE permaneçam esticadas imediata
Resolva o Problema 16.11, considerando que a aceleração a do suporte é dirigida para baixo.
Considerando que a massa de um barril cheio somado com seu conteúdo tem uma massa combinada de 100 k g . Um cilindro C é ligado ao barril na altura h = 550 m m como mostra figura. Sabendo que μ s = 0,
O suporte mostrado na figura é usado para transportar uma lata cilíndrica de um nível de elevação para outro. Sabendo que μ s = 0,25 entre a lata e o suporte, determine (a) a intensidade da aceleração
Uma placa retangular uniforme tem uma massa de 5 k g e é mantida na posição por três cordas como mostrado na figura. Sabendo que θ = 30 ° , determine, imediatamente depois da corda CF ter sido cortada