Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas de Revisão - Ex. 132

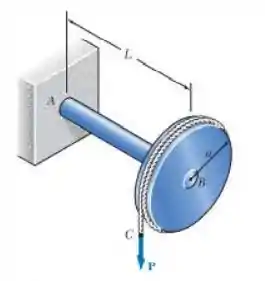
Um disco de raio a foi soldado à extremidade B do eixo de aço de seção cheia A B . Um cabo é enrolado ao redor do disco e uma força vertical P é aplicada à extremida C do cabo. Sabendo que o raio do eixo é r e desprezando as deformações do disco e do cabo, mostre que a deflexão do ponto C provocada pela aplicação de P é:

δ C = P L 2 3 E I 1 + 1,5   E r 2 G L 2  

Passo 1

Fala, galerinha. Beleza? Bora pra mais um exercício.

Para provarmos esta proposição vamos começar encontrando a torção, temos:

T = P a

Em seguida, vamos determinar a energia de deformação para a torção. Ela é dada por:

U t = T 2 L 2 G J U t = P 2 a 2 L 2 G J

E então, para determinarmos a energia de deformação para o momento fletor, temos, primeiro que o momento fletor determinar o momento fletor:

M = P v

Logo, temos que a energia de deformação vai ser:

U b = ∫ 0 L M 2 2 E I   d v = ∫ 0 L P 2 v 2 2 E I   d v U b = + P 2 L 3 6 E I

Passo 2

Por fim, vamos lembrar que a a energia de deformação é uma grandeza escalar, portanto, a máxima energia de deformação vai ser a soma das energias de deformação. Fica assim:

U = U b + U t U = P 2 a 2 L 2 G J + P 2 L 3 6 E I

Podemos associar a deflexão no ponto C à energia de deformação total através da seguinte relação:

1 2 P   δ C = U 1 2 δ C = P 2 a 2 L 2 G J + P 2 L 3 6 E I δ C = P L 2 3 E I 1 + 1,5   E r 2 G L 2

É isso, galera Bora pra próxima?

Resposta

δ C = P L 2 3 E I 1 + 1,5   E r 2 G L 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usando E = 200G P a , determinar, por meio aproximado, a máxima energia de deformação que pode ser acumulada pela porção A B de 240m m , da barra de controle mostrada, se a tensão normal admissível é
Na treliça mostrada, todos os membros são feitos do mesmo material e têm seções transversais uniformes, com as áreas indicadas. Determinar a energia de deformação da treliça, quando a carga P é aplica
Cada uma das barras de treliça mostrada é feita de alumínio e tem a seção transversal com as áreas indicadas. Usando E = 72G P a , determinar a energia de deformação da treliça para o carregamento mos
Na treliça mostrada, todos os membros são feitos do mesmo material e têm seções transversais uniformes, com as áreas indicadas. Determinar a energia de deformação da treliça, quando a carga P é aplica
Cada uma das barras de treliça mostrada é feita de aço e tem a seção transversal com as áreas indicadas. Usando E = 200G P a , determinar a energia de deformação da treliça para o carregamento mostrad