Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas de Revisão - Ex. 127

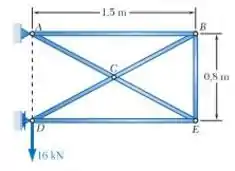
Cada elemento da treliça mostrada é feito de aço e tem uma área de seção transversal de 400   m m 2 . Usando E = 200   G P a , determine a deflexão (o deslocamento) no ponto D causado pela carga de 16   k N .

Passo 1

Fala, galerinha. Beleza? Bora pra mais um exercício.

Neste exercício, temos que determinar a deflexão (o deslocamento) no ponto D causado pela carga de 16   k N . Para isso, vamos, primeiro, eboçar o D C L :

Em seguida, vamos utilizar as equações de equilíbrio, aplicadas sobre toda a treliça, para determinarmos as reações de apoio:

∑ M A = 0 D x = 0

E também, para as forças verticais e horizontais, temos:

∑ F x = 0 A x + B x = 0 A x = 0

∑ F y = 0 A y - 16 = 0 A x = 16   k N

Em seguida, a partir do nó em A , vamos determinar as forças que atuam em cada braço da treliça. Por semelhança de triângulos, temos:

F A B 15 = F A C E 17 = 16 0,8

Assim:

F A B = - 30   k N   c o m p r e s s ã o F A C E = 3 4   k N   ( t r a ç ã o )  

Por simetria, temos que:

F D E = - 30   k N   c o m p r e s s ã o F B C D = 34   k N   ( t r a ç ã o )

E então, a partir do nó B , vamos utilizar as equações de equilíbrio:

∑ F y = 0 - 8 17 F A C E - F B E = 0 - 8 17 34 - F B E = 0 F B E = - 16   k N   c o m p r e s s ã o

Passo 2

E então, vamos determinar a energia de deformação. Ela é dada por:

U = ∑ F i 2 L i 2 E A = 1 2 E A ∑ F i 2 L i

A parte constante sai do somatório, logo, vamos calculá-la:

1 2 E A = 1 2 ( 200 × 10 9 ) ( 400 × 10 - 6 ) = 1 160 × 10 6

E para o somatório ∑ F i 2 L i , vamos preencher uma tabela com os dados para cada braço da treliça. Fica assim:

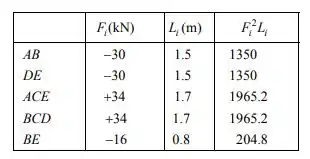
Portanto:

∑ F i 2 L i = 6,8352 × 10 9   N 2

Assim, a energia máxima de deformação é dada por:

U = 1 160 × 10 6 6,8352 × 10 9 U = 42,72   N ∙ m

Passo 3

Por fim, para determinarmos a deflexão no ponto B , vamos utilizar o principio do trabalho e energia, que é dado por:

1 2 P δ = U

Substituindo:

1 2 16 × 10 3 δ = 42,72 δ = - 5,34 × 10 - 3   m

É isso, galera Bora pra próxima?

Resposta

δ = - 5,34 × 10 - 3   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma barra de alumínio ( E = 70G P a ;α = 23,6.10 - 6° C - 1 ) e uma haste de aço ( E = 200G P a ;α = 11,7.10 - 6° C - 1 ) tem as dimensões mostradas, a uma temperatura de 20°C. A haste de aço é aqueci
Em um teste de tração, uma barra de 20 m m de diâmetro, feita de um plástico que acaba de ser desenvolvido, é submetida a uma força P de intensidade 6k N . Sabendo-se que um alongamento de 14 m m e um
Uma linha de inclinação 4 : 10 é desenhada sobre uma placa de latão-amarelo de 150 m m de largura e 6,35m m de espessura. Usando a tabela apêndice B, para esse material, determinar a inclinação da lin
A barra de alumínio AD é ajustada a uma camisa, onde é aplicada uma pressão hidrostática de 40M P a , no trecho BC de comprimento igual a 300 m m . Sabendo-se que E = 70G P aev = 0,36 , determinar:A v
Para o quadrado do P r o b . 2.70 , determinar a variação percentual da inclinação da diagonal DB devida a pressurização do vaso.