Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 25
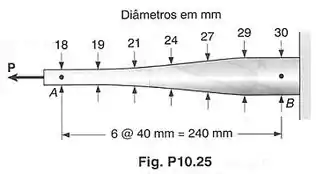
Usando , determinar, por meio aproximado, a máxima energia de deformação que pode ser acumulada pela porção de , da barra de controle mostrada, se a tensão normal admissível é .
Passo 1
E aí, queridas e queridos! Como está a vida? Muita matéria para estudar, né? Mas relaxa que essa questão passo a passo vai com certeza te ajudar a acelerar seus estudos!
O enunciado pede para a gente calcular a máxima energia de deformação de uma barra com um diâmetro variável! é a máxima energia que a barra pode ter antes de se deformar permanentemente.
A figura abaixo mostra como é essa barra com diâmetro variável.
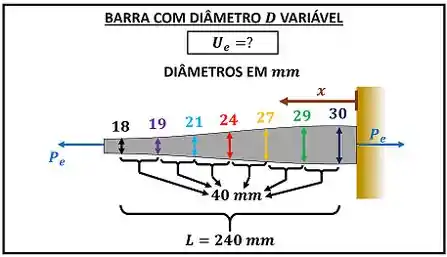
Para calcular a energia de deformação máxima , precisamos encontrar antes o valor da máxima força que a barra suporta! Para achar esse valor, se liga na dica: em qualquer questão de barras submetidas a cargas axiais, a força máxima que a barra suporta é igual a tensão normal admissível vezes a área da menor seção transversal da barra!
vale segundo o enunciado.
Como podemos ver na figura, a área mínima é a área com diâmetro de !
Para achar a partir da força precisamos calcular a integral abaixo.
onde é a distância entre um ponto qualquer da barra e a parede, é a área da seção transversal da barra e é o módulo de elasticidade da barra. O enunciado informa o valor de .
Os termos e são constantes e, portanto não interferem na integral. No entanto, a área da seção transversal da barra varia ao longo do eixo . Logo, para integrar, nós teríamos que ter uma equação de em função de .
O problema é que só conhecemos o valor do diâmetro da barra em apenas 7 pontos que estão separados por uma distância . Isso quer dizer que não sabemos como a área varia exatamente com . Logo, precisamos calcular a integral de forma aproximada!
Antes de aproximar a integral, vamos transformá-la.
Passo 2
Nesse passo, a gente vai transformar a integral que temos para conseguir fazer um cálculo aproximado dela!
Primeiro, temos que lembrar que a área vale:
Substituindo a equação de e na integral, achamos.
, e são constantes. Logo, podemos ser tirados da integral.
Desse jeito, só restou o diâmetro dentro da integral, porque ele é o único termo que varia com . O problema é que não temos uma equação de em função de . Por isso, vamos ter que calcular a integral de forma aproximada, usando o valor dos 7 diâmetros que temos.
No próximo passo veremos como fazer essa aproximação.
Passo 3
Para aproximar a integral, usaremos a regra de Simpson. Essa regra diz que, para fazer o cálculo aproximado da integral de uma função qualquer , conhecendo o valor da função em apenas 7 pontos, podemos usar a fórmula abaixo.
é a distância entre os 7 pontos. No nosso caso, vale:
e são os limites de integração da função. No nosso caso, e valem:
é a função que queremos integrar. No nosso caso, vale:
Substituindo tudo isso na regra de Simpson, encontramos:
Passando os diâmetros para metro através da divisão dos seus valores em por e substituindo esses valroes convertidos na integral, podemos calcular o valor da integral.
Fazendo as contas a integral dá:
Aeee, resolvemos a integral. Mas calma, porque o exercício ainda não acabou.
No próximo passo a gente vai usar esse valor para achar .
Passo 4
Nesse passo vamos, enfim, achar o valor de . Para isso, temos que substituir todos os dados que temos na equação de .
Antes disso, precisamos converter de para , multiplicando seu valor por .
Além disso, precisamos converter também o valor de de para , multiplicando seu valor por .
Por fim, nós temos que calcular .
Substituindo tudo isso na fórmula de , achamos: