Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 45

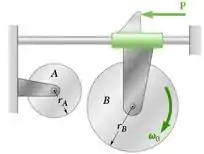
O disco B tem uma velocidade angular ω 0 quando ele é posto em contato com o disco A, que está em repouso. Mostre que (a) as velocidade angulares finais dos discos são independentes do coeficiente de atrito μ k entre os discos desde que μ k ≠ 0 , (b) a velocidade angular final do disco B depende somente de ω 0 e da razão das massas mA e mB dos dois discos.

Passo 1

Enquanto o escorregamento ocorre:

F = μ k N = μ k P

Disco A:

+ Σ M A = Σ M A eff :             F r A = I - A α A

μ k P r A = 1 2 m A r A 2 α A

α A = 2 P μ k m A r A

Passo 2

Disco B:

+ Σ M B = Σ M B eff :             F r B = I - B α B

μ k P r B = 1 2 m B r B 2 α B

α B = 2 P μ k m B r B

Passo 3

Escorregar termina quando

ω A r A = ω B r B

a A t r A = ω 0 - α B t r B

α A r A + α B r B t = ω 0 r B

Substitua das Eqs. (1) + (2):

2 P μ k m A r A r A + 2 P μ k m B r B r B t = ω 0 r B

2 P μ k 1 m A + 1 m B t = ω 0 r B

t = ω 0 r ˙ B 2 P μ k ∙ 1 1 m A + 1 m B

t = ω 0 r ˙ B 2 P μ k ∙ m A m B m A + m B

Passo 4

Eq. (3)

ω A = a A t 2 P μ k m A r A ∙ ω 0 r B 2 P μ k ∙ m A m B m A + m B

ω A = r B r A ∙ m B m A + m B ω 0

( ω A é independente de μ k , QED)

Eq. (4):

ω B = ω 0 - α B t = ω 0 - 2 P μ k m B r B ∙ ω 0 r B 2 P μ k ∙ m A m B m A + m B

ω B = ω 0 1 - m A m A + m B

ω B = ω 0 m A + m B - m A m A + m B = ω 0 m B m A + m B

ω B = ω 0 m A m B + 1

ω B depende apenas de ω 0 e m A m B (QED)

Resposta

ω B = ω 0 m A m B + 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um quadro de 2 m é colocado em um caminhão com uma extremidade repousando sobre um bloco preso no piso e a outra apoiada em uma divisória vertical. Determine a máxima aceleração admissível do caminhão
Desenhe os diagramas de esforço cortante e de momento fletor da barra AB do Problema 16.17.PROBLEMA 16.17 Três barras, cada uma de massa de 4 kg, são soldadas juntas e unidas por pinos a duas hastes d
Um sistema de transporte é equipado com painéis verticais, e uma barra A B de 300 m m e de massa 2,5 k g é depositada entre dois painéis como mostra a figura. Se a barra permanece na posição mostrada
Um sistema de transporte é equipado com painéis verticais, e uma barra A B de 300 m m e de massa 2,5 k g é depositada entre dois painéis como mostra a figura. Sabendo que a aceleração do sistema é 1,5
Para uma placa rígida em translação, mostre que o sistema das forças efetivas consiste de vetores ∆ m i a - unidos às várias partículas da placa, onde a - é a aceleração do centro de massa G da placa.