Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 23
Para uma placa rígida em translação, mostre que o sistema das forças efetivas consiste de vetores unidos às várias partículas da placa, onde é a aceleração do centro de massa G da placa. Mostre também, calculando sua soma e a soma de seus momentos em relação a G, que as forças efetivas são reduzidas a um único vetor ligado em G.
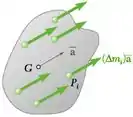
Passo 1
Gurizada notem que como a placa está em translação, cada partícula tem a mesma aceleração de G, ou seja, . As forças efetivas consistem em .
A soma desses vetores é:
Então temos:
A soma dos momentos sobre G é:
Passo 2
Mas, , porque G é o centro de massa. Conclui-se que o membro do lado direito da Eq. (1) é zero. Assim, o momento sobre G de também deve ser zero, o que significa que sua linha de ação passa por G e que pode estar ligada em G.
Resposta
Mas, , porque G é o centro de massa. Conclui-se que o membro do lado direito da Eq. (1) é zero. Assim, o momento sobre G de também deve ser zero, o que significa que sua linha de ação passa por G e que pode estar ligada em G.