Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas de Revisão - Ex. 198
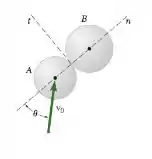
Os discos A e B com massas mA e mB, respectivamente, podem deslizar livremente em uma superfície horizontal sem atrito. O disco B está em repouso quando é atingido pelo disco A que está em movimento com a velocidade v0 em uma direção que forma um ângulo θ com a linha de impacto. Representa por e o coeficiente de restituição entre os dois discos, mostre que a componente n da velocidade de A depois do impacto é positiva se mA > emB, negativa se mA
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Como foi de fim de ano?? Preparado para voltar?? Então vamos lá Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para analisarmos a figura e dizermos quais são as componentes da velocidade. Parece muita coisa, mas é tranquilo. Partiu??
Passo 2
Ok, vamos aplicar os conceitos empregados no impacto entre dois corpos, ou seja, a colisão que ocorre em um espaço de tempo muito pequeno.
Também vamos relembrar que a quantidade de movimento linear de uma partícula foi definida como o produto de sua massa m e de sua velocidade v, assim como a aplicação do Coeficiente de Restituição, que relaciona as velocidades relativas de dois corpos antes e depois do impacto, e o Princípio do Impacto Central Obliquo.
A conservação de energia de A e B é dada por:
Na direção normal, temos que:
Eaii?? Chegou bem até aqui?? Então bora substituir os valores e continuar nossa conta.
As velocidades relativas são:
Passo 3
Pronto!! Agora é só fazermos umas matemágicas aí pra achar o resultado!!