Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 14.Problemas - Ex. 25

14.25. Uma ogiva de 6 kg que se move a uma velocidade v0 (12 m/s)i (10

m/s)j (400 m/s)k explode no ponto D em três fragmentos, A, B e

C, que têm massa de, respectivamente, 2,5 kg, 2 kg e 1,5 kg. Sabendo

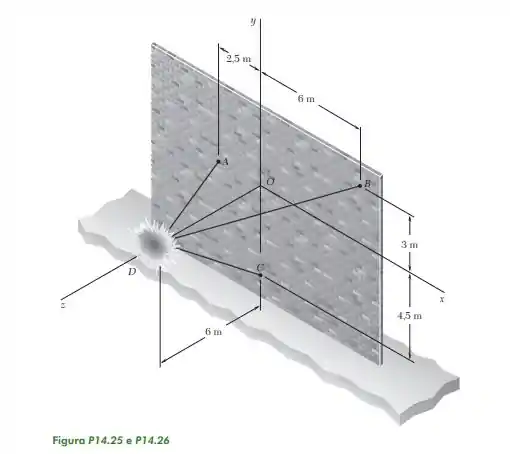
que os fragmentos atingem a parede vertical nos pontos indicados,

determine a velocidade de cada fragmento imediatamente após a explosão.

Passo 1

Na resolução desse exercício vamos usar conservação de momento. O momento da ogiva é numericamente igual a soma do momento das três partículas:

L o g i v a = L A + L B + L C

Então

m o g i v a ⋅ v 0 = m A ⋅ v A + m B ⋅ v B + m C ⋅ v C

Passo 2

Na imagem, o ponto D, o ponto central onde x , y , z = ( 0,0 , 0 ) e os pontos de colisão formam triângulos, e esses triângulos vão nos ajudar a calcular a velocidade de cada partícula.

Veja por exemplo, para a partícula A , temos o triângulo D O A - :

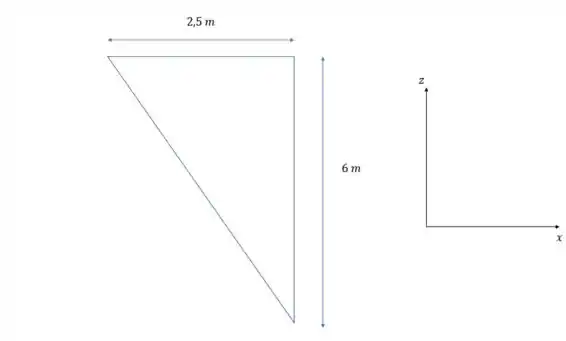
Então podemos usar trigonometria básica para determinar que a velocidade dessa partícula é:

v A = - sin ⁡ θ   i ^ - cos ⁡ θ   k ^   v A

Veja que a partícula se deslocou para o sentido negativo de x e de z .

Logo

v A → = - 2,5 6 2 + 2,5 2   i ^ - 6 6 2 + 2,5 2   k ^   v A = - 2,5 6,5   i ^ - 6,5 6,5   i ^   v A = - 0,38   i ^ - 0,92   k ^ v A  

Podemos fazer analogamente para as outras partículas:

v B → = 6 6 2   i ^ + 3 3 5   j ^ - 6 6 2 k ^ v B = 0,71   i ^ + 0,45   j ^ - 0,71   k ^ v B

v C → = - 4,5 3 3   j ^ - 6 3 3   k ^ v C = - 0,87   j ^ - 1,15   k ^ v C

Passo 3

Nós podemos decompor esse movimento em termos das componentes cartesianas i ^ , j ^ e k ^ .

Vamos começar com a componente em i ^ . Nessa componente sabemos que:

L o g i v a   i ^ = L A + L B + L C i ^

L o g i v a   i ^ = 6 ⋅ 12 = 72

Então

2,5 ⋅ v A + 2 ⋅ v B + 1,5 ⋅ v C i ^ = 72

Usando os valores que a gente obteve no passo anterior temos:

- 2,5 ⋅ 0,38 ⋅ v A + 2 ⋅ 0,71 ⋅ v B = 72

Agora na componente j ^ temos:

L o g i v a   j ^ = 6 ⋅ ( - 10 ) = - 60

Então

2,5 ⋅ v A + 2 ⋅ v B + 1,5 ⋅ v C j ^ = - 60

Temos:

2 ⋅ 0,45 ⋅ v B - 1,5 ⋅ 0,87 ⋅ v C = - 60

E por fim a componente k ^ :

L o g i v a   k ^ = 6 ⋅ ( - 400 ) = - 2400

Então

2,5 ⋅ v A + 2 ⋅ v B + 1,5 ⋅ v C k ^ = - 2400

Temos:

- 2,5 ⋅ 0,92 ⋅ v A + 2 ⋅ 0,71 ⋅ v B + 1,5 ⋅ 1,15 ⋅ v C = - 2400

Passo 4

Agora temos 3 equações com 3 incógnitas. Isso significa que podemos montar um sistema linear e determinar o valor de todas as incógnitas:

- 2,5 ⋅ 0,38 ⋅ v A + 2 ⋅ 0,71 ⋅ v B = 72                                                                                                   ( I ) 2 ⋅ 0,45 ⋅ v B - 1,5 ⋅ 0,87 ⋅ v C = - 60                                                                                                           ( I I ) - 2,5 ⋅ 0,92 ⋅ v A + 2 ⋅ 0,71 ⋅ v B + 1,5 ⋅ 1,15 ⋅ v C = - 2400           ( I I I )

Agora vamos isolar v B na equação (I):

- 2,5 ⋅ 0,38 ⋅ v A + 2 ⋅ 0,71 ⋅ v B = 72

v B = 72 + 0,95 v A 1,42

Vamos substituir isso na equação (II)

2 ⋅ 0,45 ⋅ v B - 1,5 ⋅ 0,87 ⋅ v C = - 60

2 ⋅ 0,45 ⋅ 72 + 0,95 v A 1,42 - 1,5 ⋅ 0,87 ⋅ v C = - 60

Então

v C = 60 + 64,8 + 0,855   v A 1,42 1,3

Finalmente podemos substituir tudo isso na equação (III)

2,5 ⋅ 0,92 ⋅ v A + 2 ⋅ 0,71 ⋅ 72 + 0,95 v A 1,42 + 1,5 ⋅ 1,15 ⋅ 60 + 64,8 + 0,855   v A 1,42 1,3 = 2400        

Agora podemos descobrir o valor de v A

1,84 ⋅ v A + 72 + 0,95 v A + 79,61 + 60,55 + 0,8   v A = 2400        

v A = 2400 - 72 - 79,61 - 60,55 1,84 + 0,95 + 0,8 = 2187,84 3,59 = 609,43 m s        

Agora podemos definir v B e v C

v B = 72 + 0,95 v A 1,42

v B = 72 + 0,95 609,43 1,42 = 458,42 m s

E

2 ⋅ 0,45 ⋅ v B - 1,5 ⋅ 0,87 ⋅ v C = - 60

2 ⋅ 0,45 ⋅ ( 458,42 ) - 1,5 ⋅ 0,87 ⋅ v C = - 60

v C = 60 + 412,578 1,724 = 274,117 m s

Passo 5

Agora vamos usar esses valores para definir a velocidade como vetor. Lembra do que fizemos lá no começo? A gente separou as componentes de cada vetor velocidade.

v A → = - 0,38   i ^ - 0,92   k ^ v A

v A → = - 0,38   i ^ - 0,92   k ^ 609,43 = - 231,58   i ^ - 560,67   k ^ m s  

v B → = 0,71   i ^ + 0,45   j ^ - 0,71   k ^ v B

v B → = 0,71   i ^ + 0,45   j ^ - 0,71   k ^ 458,42 = 325,47   i ^ + 206,3   j ^ - 325,48 k ^ m s

v c → = - 0,87   j ^ - 1,15   k ^ v C

v c → = - 0,87   j ^ - 1,15   k ^ 274,117 = - 238,48   j ^ - 315,23   k ^ m s

Resposta

v A → = - 231,58   i ^ - 560,67   k ^ m s  

v B → = 325,47   i ^ + 206,3   j ^ - 325,48 k ^ m s

v c → = - 238,48   j ^ - 315,23   k ^ m s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O foguete utilizado para lançar a espaçonave de 540k g do Problema 14.97 é reprojetado para incluir dois estágios, A e B, cada um com massa 9,5 Mg, incluindo 8,9 Mg de combustível. O combustível é nov
Para a espaçonave e o foguete de lançamento de dois estágios do Problema 14.98, determine a altitude em que (a) o estágio A do foguete é liberado, (b) o combustível de ambos os estágios terá sido cons
Em um foguete, a energia cinética transmitida ao combustível consumido e ejetado é perdida no que concerne à propulsão do foguete. A potência útil é igual ao produto da força disponível para impulsion
Em um avião a jato, a energia cinética transmitida aos gases de exaustão é perdida no que concerne à propulsão do avião. A potência útil é igual ao produto da força disponível para impulsionar o avião
Uma espaçonave de 540k g é montada no topo de um foguete de massa 19M g , incluindo 17,8M g de combustível. Sabendo que o combustível é consumido a uma taxa de 225k g / s e que a exaustão se dá com um