Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 12.Problemas - Ex. 48

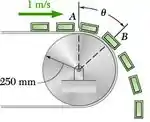
Uma série de pequenos pacotes, cada um com a massa de 0,5 kg, é descarregada de uma correia transportadora como mostrado na figura. Sabendo que o coeficiente de atrito estático entre cada pacote e a correia transportadora é 0,4, determine (a) a força exercida pela esteira no pacote exatamente depois que ele tenha passado no ponto A, (b) o ângulo θ definindo o ponto B onde os pacotes têm o primeiro escorregamento relativo na correia.

Passo 1

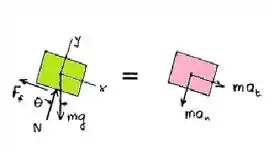
Suponha que o pacote não escorregue então temos as seguintes considerações:

a t = 0 ,           F f ≤ μ s N

Na parte curva da correia

a n = v 2 ρ = 1   m/ s 2 0.250   m = 4   m/ s 2

Para qualquer ângulo θ

+ ↗ Σ F y = m a y :         N - m g cos ⁡ θ = - m a n = - m v 2 ρ

N = m g cos ⁡ θ - m v 2 ρ

+ ↘ Σ F x = m a x :     - F f + m g sin ⁡ θ = m a t = 0

F f = m g sin ⁡ θ

Passo 2

  1. No ponto A,

    2. θ = 0 °

    N = 0.5 9.81 1.000 - 0.5 4

    Passo 2

  2. No ponto B,

F f = μ s N

m g sin ⁡ θ = μ s m g cos ⁡ θ - m a n

sin ⁡ θ = μ s cos ⁡ θ - a n g = 0.40 cos ⁡ θ - 4 9.81

Quadrado e usando identidades trigonométricas,

1 - cos 2   θ = 0.16   cos 2   θ - 0.130479 cos ⁡ θ + 0.026601

1.16   cos 2   θ - 0.130479 cos ⁡ θ - 0.97340 = 0

cos ⁡ θ = 0.97402

Verifique se a embalagem não se separa da correia.

N = F f μ s = m g sin ⁡ θ μ s                       N > 0 .

Resposta

a)   N = 2.905   N

b)   θ = 13.09 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O bloco deslizante B está limitado a mover-se dentro da ranhura lisa. Ele está conectado a duas molas, cada uma com uma rigidez k = 30N / m . As molas estão originalmente estedindas 0,5m quando s = 0
O carrinho B , de 10k g , está apoiado em roletes de dimensão desprezível. Se uma maleta A de 5k g é lançada horizontalmente sobre o carrinho a 3m / s quando ele está em repouso, determine o período d
A estaca P tem massa de 800k g e está sendo enterrada na areia solta por um martelo C , de 300k g , que é deixado cair de uma distância de 0,5m a partir do topo da estaca. Determine a velocidade inici
Um homem calçando patins de gelo lança um bloco de 8k g a uma velocidade inicial de 2m / s , medida relativamente a ele mesmo, na direção mostrada. Se ele está originalmente em repouso e completa o la
Uma bola tem massa m e é deixada cair sobre uma superfície a partir de uma altura h . Se o coeficiente de restituição entre a bola e a superfície é e , determine o tempo necessário para a bola parar d