Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 97
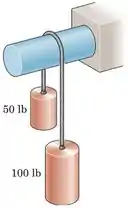
Qual é o coeficiente mínimo de atrito entre o cabo e o eixo fixo que impedirá os cilindros desequilibrados de se moverem?
Passo 1
O exercício pede que a gente determine coeficiente mínimo de atrito entre o cabo e o eixo fixo que impedirá os cilindros desequilibrados de se moverem
Temos
Passo 2
Então
Resposta
Exercícios de Livros Relacionados
Determine a menor força P que causará a iminência de movimento. A caixa e a roda têm uma massa de 50k g e 25k g , respectivamente. O coeficiente de atrito estático entre a caixa e o piso é μ s = 0,2 ,
Sabendo que o coeficiente de atrito entre o bloco de 15 kg e o plano inclinado é μ s = 0,25 , determine ( a ) o menor valor de P necessário para se manter o bloco em equilíbrio, ( b ) o valor correspo
Os coeficientes de atrito são μ s = 0,4 e μ k = 0,3 entre todas as superfícies de contato. Determine a menor força P necessária para iniciar o movimento do bloco de 30 kg se o cabo AB ( a ) está ligad
Determine o intervalo de valores de P para o qual o equilíbrio do bloco mostrado na figura é mantido.
Considerando apenas valores de θ menores que 90°, determine o menor valor de θ solicitado para o qual o movimento do bloco para a direita é iminente quando ( a ) W = 340 N, ( b ) W = 450 N.