Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 105
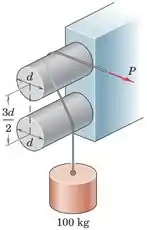
Calcule a força horizontal P necessária para elevar a carga de 100 kg. O coeficiente de atrito entre o cabo e as barras fixas é de 0,40.
Passo 1
O enunciado pede que a gente determine a força horizontal P necessária para elevar a carga de 100 kg. O coeficiente de atrito entre o cabo e as barras fixas é de 0,40.
Da expressão
Passo 2
Podemos escrever a expressão tensão T2 como
Uma vez que a força P está iniciando o aumento da carga, podemos escrever a expressão (1) como
Passo 3
Onde o peso da carga é
O coeficiente de atrito é
Enquanto o ângulo é
Onde
Passo 4
Vamos substituir e na expressão acima para obter
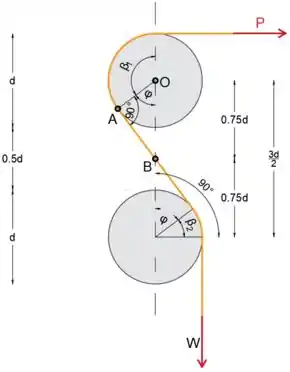
Usando a regra do seno, podemos determinar o ângulo do triângulo OAB
Usando o teorema de Pitágoras, podemos determinar o comprimento
Passo 5
Agora podemos determinar o ângulo
Vamos substituir por seu valor na expressão (3)
Finalmente, vamos determinar a força P, colocando toda a expressão de valores desconhecidos (2)