Dois eixos maciços e as engrenagens mostradas são usadas para transmitir de um motor em , que gira a uma frequência de , a uma máquina-ferramenta em . Sabendo-se que cada eixo tem um diâmetro de , determine a máxima tensão de cisalhamento: (a) no eixo ; (b) no eixo .
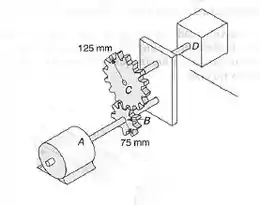
Passo 1
a) Queremos a máxima tensão no eixo . Temos esses dados sobre esse eixo:
- frequência de rotação:
- potência transmitida:
- diâmetro: , logo o raio é:
Vem comigo!
Passo 2
Vamos achar o torque nesse eixo, pela relação:
Substituindo os dados do nosso problema:
Passo 3
Para um eixo maciço, temos que:
A gente consegue escrever uma relação entre a tensão máxima, o torque produzido nessa situação e o raio do eixo, pela expressão:
Substituindo nossos dados:
Passo 4
b) Agora a gente precisa achar a tensão máxima no eixo . Para isso vamos descobrir a torção que está ocorrendo nesse eixo.
Como temos uma transmissão de potência com engrenagens entre o eixo e o eixo , podemos usar essa relação para achar o torque em :
O raio da engrenagem em é , e em é . Substituindo isso e o torque que a gente achou para :
Passo 5
Podemos agora usar essa relação de novo:
Mas estamos no eixo , então:
Substituindo os nossos dados:
Resposta
(a)
(b)