Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 12.Problemas - Ex. 40

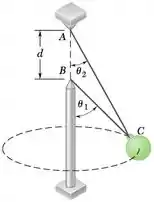
Dois fios AC e BC estão amarrados a uma esfera de 7 kg que roda com uma velocidade escalar v no círculo horizontal mostrado na figura. Sabendo que θ 1 = 55° e θ 2 = 30° e que d = 1,4 m, determine o intervalo de valores de v para os quais ambos os fios permanecem tracionados.

Passo 1

Primeiro notamos

a C = a n = v C 2 ρ

onde

ρ = l tan ⁡ 55 °

e

ρ = d + l tan ⁡ 30 °

Então

ρ = d + ρ tan ⁡ 55 ° tan ⁡ 30 °

ou

ρ = 1.4  m 1 tan ⁡ 30 ° - 1 tan ⁡ 55 ° = 1.35680  m

← + Σ F x = m C a C :         T C A sin ⁡ 30 ° + T C B sin ⁡ 55 ° = m C v C 2 ρ

+ ↑ Σ F y = 0 :         T C A cos ⁡ 30 ° + T C B cos ⁡ 55 ° - W C = 0

ou

T C A cos ⁡ 30 ° + T C B cos ⁡ 55 ° = m C g

Passo 2

Caso 1: TCA = 0:

E q .   2 ⇒ T C B = m C g cos ⁡ 55 °

Substituindo na Eq. (1)

m C g cos ⁡ 55 ° sin ⁡ 55 ° = m C v C 2 ρ

ou

( v C 2 ) T C A = 0 = 1.35680   m 9.81   m tan ⁡ 55 °

ou

( v C ) T C A = 0 = 4.36   m/s

Agora nós formamos

cos ⁡ 30 ° 1 - sin ⁡ 30 ° 2

T C B sin ⁡ 55 ° cos ⁡ 30 ° - T C B cos ⁡ 55 ° sin ⁡ 30 ° = m C v C 2 ρ cos ⁡ 30 ° - m C g sin ⁡ 30 °

ou

T C B sin ⁡ 25 ° = m C v C 2 ρ cos ⁡ 30 ° - m C g sin ⁡ 30 °

( v C ) max   ocorre quando T C B = ( T C B ) max , o que ocorre quando T C A = 0 .

( v C ) max = 4.36  m/s  e fio AC ficará tenso se v C < 4.36  m/s.

Passo 3

Caso 2: TCB = 0:

E q .   2 ⇒ T C A = m C g cos ⁡ 30 °

Substituindo na Eq. (1)

m C g cos ⁡ 30 ° sin ⁡ 30 ° = m C v C 2 ρ

ou

( v C 2 ) T c g = 0 = 1.35680   m 9.81   m / s 2   tan   30 °

ou

( v C ) T C g = 0 = 2.77   m/s

Passo 4

Agora nós formamos

cos ⁡ 55 ° 1 - sin ⁡ 55 ° 2

T C A sin ⁡ 30 ° cos ⁡ 55 ° - T C A cos ⁡ 30 ° sin ⁡ 55 ° = m C v C 2 ρ cos ⁡ 55 ° - m C g sin ⁡ 55 °

ou

- T C A sin ⁡ 25 ° = m C v C 2 ρ cos ⁡ 55 ° - m C g sin ⁡ 55 °

( v C ) min   ocorre quando T C A = ( T C B ) max , o que ocorre quando T C B = 0 .

( v C ) min = 2.77  m/s  e fio BC ficará tenso se v C < 2.77  m/s.

Resposta

Ambos os fios estão tensos então 2.77   m/s   < v < 4.36  m/s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A rampa de rolagem livre tem massa de 60k g . A caixa, cuja massa é 40k g , desliza, partindo do repouso em A , 4,5m rampa abaixo até B . Determine a velocidade da rampa quando a caixa atingir B . Sup
Uma bola de 1k g está viajando horizontalmente a 20m / s quando atinge um bloco B de 10k g que está em repouso. Se o coeficiente de restituição entre A eB é e = 0,6 e o coeficiente de atrito cinético
O bloco deslizante B está limitado a mover-se dentro da ranhura lisa. Ele está conectado a duas molas, cada uma com uma rigidez k = 30N / m . As molas estão originalmente estedindas 0,5m quando s = 0
O carrinho B , de 10k g , está apoiado em roletes de dimensão desprezível. Se uma maleta A de 5k g é lançada horizontalmente sobre o carrinho a 3m / s quando ele está em repouso, determine o período d
A estaca P tem massa de 800k g e está sendo enterrada na areia solta por um martelo C , de 300k g , que é deixado cair de uma distância de 0,5m a partir do topo da estaca. Determine a velocidade inici