Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 8.Problemas - Ex. 20
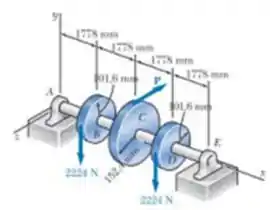
As duas de são vertical e a força P é paralela ao eixo Sabendo que . determine o menor diâmetro admissível para eixo cheio AE.
Passo 1
Então gurizada, vamos fazer algumas conversões para facilitar nossos cálculos?! Vamos começar, desenhando o esboço do diagrama de corpo livre.
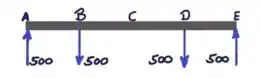
Força do plano vertical
Torques: =
Passo 2
As seções críticas estão em ambos os lados do disco C, considere o esboço abaixo :D
Passo 3
Para as forças do plano horizontal temos:
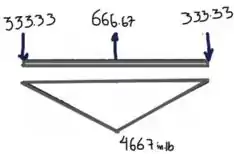
Resposta
4.
Exercícios de Livros Relacionados
Determine o menor diâmetro admissível para o eixo de seção cheia ABCD.sabendo que τ a d m = 60M P a e que raio do disco B é r = 80m m .
A força de 4k N é paralela ao eixo x e a força Q é paralela ao eixo z . O eixo AD é vazado. Sabendo que o diâmetro interno é metade do diâmetro externo e que τ a d m = 60M P a , determine o menor diâm
As forças vertical P 1 e horizontal P 2 são aplicadas aos discos soldados ao eixo de seção cheia AD conforme mostrado. Sabendo que o diâmetro do eixo é de 1,75i n e que τ a d m = 8k s i , determine a
Sabendo que σ a d m = 165M P a e τ a d m = 100M P a selecione o perfil de mesa larga mais econômico que deverá ser utilizado para suportar o carregamento mostrado. () Determine os valores a serem espe
43. A viga tem seção transversal retangular e está sujeita às cargas mostradas. Determine as tensões principais desenvolvidas no ponto A e no ponto B , localizado imediatamente à esquerda da carga de