Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 8.Problemas - Ex. 15

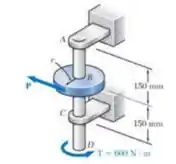
Determine o menor diâmetro admissível para o eixo de seção cheia ABCD.sabendo que τ a d m = 60   M P a e que raio do disco B é r = 80   m m .

Passo 1

e aí galerinha, vamos começar nossos cálculos:

Σ M e i x o = 0 :   T - P r   = 0       P = T r = 600 80   ×   10 - 3 = 7,5 × 10 3

R A = R C = 1 2   P = 3,75   ×   10 3   N

M B = ( = 3,75   ×   10 3 ) ( = 150   ×   10 - 3 ) = 562,6   N   ⋅   m

Passo 2

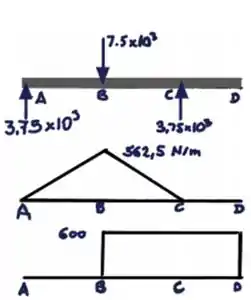
Momento fletor: (Ver desenho).

Torque: (ver desenho).

A seção crítica encontra-se no ponto B.

M = 562,5   N   × m , T = 600   N × m

J c = π 2 c 3 = M 2 + T 2 t u d o t t u d o

c 3 = 2 π   M 2 + T 2 t t u d o = 2 π 562,2 2 + 600 2 60   × 10 6 = 8,726   ×   10 - 6   m 3

c = 20,58   × 10 - 3   m d = 2 c = 41,2 × 10 - 3   m

d = 41,2   m m

Resposta

d = 41,2   m m .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os eixos de seção transversal cheia ABC e DEF e as engrenagens mostradas são utilizados para transmitir 20h p do motor M para uma máquina-ferramenta conectada ao eixo DEF. Sabendo que o motor gira a 2
Considerando que eixo ABC do Problema 8.27 é vazado e tem um diâmetro externo de 50m m ,determine o maior diâmetro inteiro admissível para o eixo
O eixo de seção cheia AB rotaciona a 600r p m e transmite 80k W a partir do motor M para a máquina-ferramentas conectadas à engrenagem F.Sabendo que τ a d m= 60M P a ,determine o menor diâmetro permit
O eixo de seção cheia ABC e as engrenagens mostradas na figura transmitem 10k W do motor M para uma máquina-ferramenta conectada à engrenages D . Sabendo que o motor gira 240r p m e que τ a d m = 60M
Resolva o Problema 8,25 considerando que o motor gira a 360r p m .