Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 8.Problemas - Ex. 19
As forças vertical e horizontal são aplicadas aos discos soldados ao eixo de seção cheia AD conforme mostrado. Sabendo que o diâmetro do eixo é de e que , determine a maior intensidade permissível para a força .
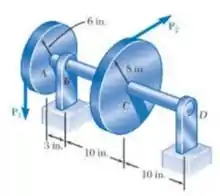
Passo 1
Então gurizada, vamos começar logo?! Iniciemos esboçando o diagrama e calculando o momento :D
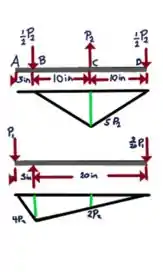
Seja em kips, temos:
Passo 2
Torque sobre a porção ABC:
Curvatura no plano horizontal:
Curvatura no plano vertical:
Passo 3
O ponto crítico está logo a esquerda do ponto C.:
Resposta
.
Exercícios de Livros Relacionados
Uma viga biapoiada com um balanço de aço laminado com um balanço de aço laminado W 920×449 suporta uma carga P conforme mostra a figura. Sabendo que P = 700k N , a = 2,5meeσ a d m = 100M P a , determi
Uma viga biapoiada com um balanço de aço laminado com um balanço de aço laminado W 920×449 suporta uma carga P conforme mostra a figura. Sabendo que P = 850k N , a = 2,0meeσ a d m = 100M P a , determi
Os problemas a seguir, se referem a um perfil de aço laminado selecionado em um problema do capítulo 5, para suportar determinado carregamento a um custo mínimo e ao mesmo tempo satisfazendo a condiçã
Sabendo que σ a d m = 160M P a e τ a d m = 100M P a selecione o perfil de mesa larga mais econômico que deverá ser utilizado para suportar carga mostrada. (b) Determine os valores a serem esperados pa
Sabendo que σ a d m = 160M P a e τ a d m = 100M P a selecione o perfil de mesa larga mais econômico que deverá ser utilizado para suportar carga mostrada. (b) Determine os valores a serem esperados pa