Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 8.Problemas - Ex. 18

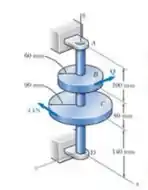
A força de 4   k N é paralela ao eixo x e a força Q é paralela ao eixo z . O eixo AD é vazado. Sabendo que o diâmetro interno é metade do diâmetro externo e que τ a d m = 60   M P a , determine o menor diâmetro externo admissível para o eixo.

Passo 1

E ai gurizada tudo bem? Partiu começar determinando o momento vem comigo :D

Σ M y = 0 :     60 × 10 - 3 Q -   ( 90 × 10 - 3 ) ( 4 × 10 3 ) = 0

Q = 6   × 10 3   N = 6   k N

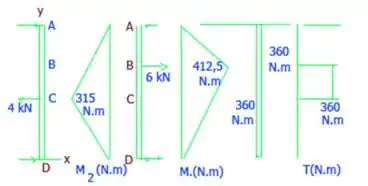
Diagramas de momento fletor e torque.

No plano xy: M z m á x i m o = 315   N ⋅ m                   e m   C

No plano yz: M x m á x i m o = 412   N ⋅ m                   e m   B

Sobre o eixo z: T m á x i m o = 360   N ⋅ m               e n t r e   B   e   C

M z = ( 100 180 ) ( 315 ) = 175   N ⋅ m

M y 2 + M z 2 + T 2 = 175 2 + 412,5 2 + 360 2 = 574,79   N ⋅ m

Passo 2

em C temos que:

M x ( 140 220 ) ( 412,5 ) = 262,5   N ⋅ m

M y 2 + M z 2 + T 2 = 315 2 + 262,5 2 + 360 2 = 545,65   N ⋅ m

O maior valor é 574,79 N ⋅ m .

t m á x i m o = m a x M y 2 + M z 2 + T 2 c J

J c = m a x M y 2 + M z 2 + T 2 t m á x i m o = 574 , , 79 60 × 10 6 = 9,5798 × 10 - 6 m 3 = 9,5798 × 10 3 m 3

J c = π 2 ( c o 4 - c i 4 ) c o = π 2 c o 3 ( 1 - c i 4 c o 4 ) = π 2 c o 3 [ 1 - ( 1 2 ) 4 ] = 1,47262   c o 3

1,47262   c o 3 = 9 , 5798 × 10 3 c o = 18,67   m m

d o = 2 c o

d o = 37,3   m m

Resposta

37,3   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o Prob. 8.23 assumindo que o eixo AB rotacionado a 720r p m
O eixo cheio AE gira a 600r p m e transmite 60h p do motor M para as máquinas-ferramentas acopladas às engrenagens G e H .Sabendo que τ a d m= 55,2M P a e que 40h p são transmitidos pela engrenagens G
Resolva o Problema 8.29 considerando que 30h p são transmitidos pela engrenagens G e 30h p são transmitidos pela engrenagens H
Uma viga de aço laminado W 250×58 suporta uma carga P conforme mostra a figura. Sabendo que P =100k N , a = 508m meσ a d m = 124,1M P a determine (a) o valor máximo da tensão normal σ m na viga,(b) o
Uma viga de aço laminado W 250×58 suporta uma carga P conforme mostra a figura.Sabendo que P =200k N , a = 254m meσ a d m = 124,1M P a determine (a) o valor máximo da tensão normal σ m na viga,(b) o v