Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.3 - Ex. 24
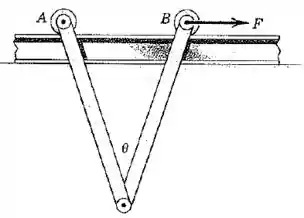
As duas barras idênticas uniformes são livremente articuladas nas extremidades inferiores e estão apoiadas nas extremidades superiores por pequenos roletes de massa desprezível que rolam sobre um trilho horizontal. Determine o ângulo permanente assumido pelas barras quando estão acelerando sob a ação de uma força constante . Encontre também as forças verticais sobre os roletes em e .
Passo 1
Vamos começar representando as forças que agem sobre cada uma das barras separadamente.
Na barra da esquerda, temos a força normal no ponto , o peso da barra e a força no contato entre as duas. A barra da esquerda está sujeita às mesmas forças, e também à força .
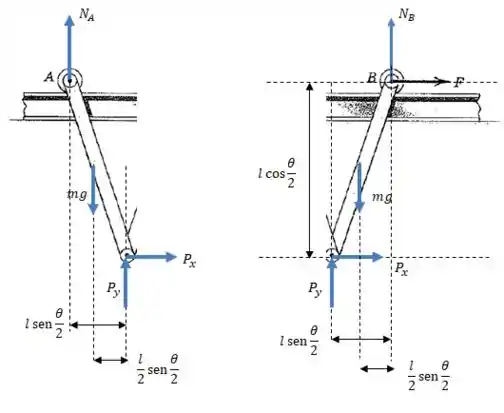
Pelo desenho do enunciado conseguimos ver que o ângulo que as barras fazem com a vertical é . (Não representamos no desenho para evitar uma bagunça.)
E vamos olhar para a soma dos momentos dessas forças em cada uma das barras, adotando o sentido horário como positivo.
Nossa referência vai ser o ponto de contato entre as duas barras, porque dessa forma vamos anular o momento da força , que é desconhecida.
Passo 2
Mas o sistema não está em equilíbrio, então a soma desses momentos não é nula!
O sistema está acelerando para a direita com aceleração , portanto as forças no desenho desenho equivalem a uma força resultante agindo no centro de massa de cada haste.
As somas e devem ser iguais ao momento dessa força . Olhando para o desenho de antes, podemos ver que esse momento é:
E assim ficamos com um sistema de duas equações:
Onde já dividimos tudo por . Vamos simplificar um pouco mais:
Agora vamos subtrair a segunda equação da primeira (para sumir com a variável ):
Agora precisamos dar um jeito nesse primeiro parênteses do lado direito. Podemos ainda explorar o fato de que o sistema está em equilíbrio na direção vertical:
Então a equação de cima fica da seguinte forma:
Passo 3
Agora queremos encontrar as forças e . Vamos aplicar a segunda lei de Newton (sobre o sistema inteiro) na direção horizontal:
Mas pelo que vimos antes:
Então:
Vamos substituir isso na primeira equação do nosso sistema do passo anterior:
Quando multiplicarmos a tangente pelo cosseno ficaremos com também do lado esquerdo, então podemos dividir por essa função:
E agora podemos calcular :
Para encontrar é só lembrar da equação que encontramos explorando o equilíbrio do sistema na vertical:
Resposta
O ângulo é , e as forças verticais são e .