Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.3 - Ex. 18

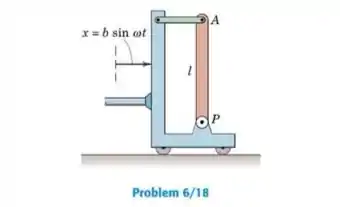
O dispositivo mostrado oscila horizontalmente de acordo com x = b s e n ω t onde ω e b são constantes. Determine e faça um gráfico da força T no elemento de ligação leve em A como uma função do tempo t. A massa da haste esbelta uniforme AP é m .

Passo 1

Primeiro vamos precisar calcular a aceleração do sistema através da equação da posição do elemento de ligação dada no enunciado (que será a aceleração de todo o dispositivo também), e depois vamos usar a equação do momento total para o ponto P.

A segunda derivada da equação é:

a = d 2 x d t 2 = - m b ω 2 s e n ω t

E a equação do momento para o ponto P:

∑ M P = m a d

Passo 2

O único momento aqui será o da força T, já que a gravidade atua no centro de massa que está na mesma linha que o ponto P. O momento resultante em relação ao ponto P é:

- T l = - m b ω 2 s e n ω t l 2

E a força T será:

T = 1 2 m b ω 2 s e n ω t

Passo 3

O gráfico terá a forma (considerando o valor de todas as constantes igual a 1)

:

Resposta

T = 1 2 m b ω 2 s e n ω t

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O reboque carregado tem uma massa de 900k g com o centro de massa em G e está preso em A a um engate em um pára-choque traseiro. Se o carro e o reboque atingem uma velocidade de 60k m / h em uma estra
O bloco A e a haste anexa têm, juntos, uma massa de 60k g e estão limitados a se deslocar ao longo da guia de 60 ° sob a ação da força aplicada de 800N . A haste uniforme horizontal possui uma massa d
Determine o módulo P e a direção θ da força necessária para transmitir uma aceleração a = 1,5m / s 2 para trás ao carrinho de mão carregado, sem rotação a partir da posição mostrada. A massa combinada
O coeficiente de atrito estático em ambas as extremidades da barra uniforme é igual a 0,40 . Determine a aceleração horizontal máxima a que o caminhão pode ter sem levar a barra a deslizar. (Sugestão:
O furgão visto por trás está viajando a uma velocidade v por uma curva de raio médio r inclinada para dentro de um ângulo θ . O coeficiente de atrito efetivo entre os pneus e a estrada é μ . Determine