Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.5 - Ex. 6
As duas esferas, cada uma com massa , estão conectadas pela mola e barras articuladas de massa desprezível. As esferas estão livres para deslizar nas guias lisas subindo a inclinação . Determine a aceleração do centro da mola.
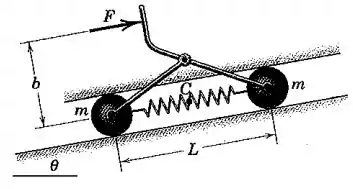
Passo 1
As esferas deslizam nas guias, indicando que não há força de atrito. Então, as únicas forças externas do sistema de esferas agindo na direção (direção de subida) são as componentes do peso de cada uma e a força , conforme destacado em verde na figura:
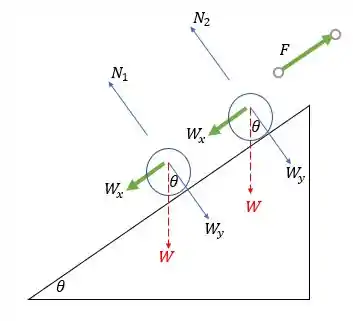
A força devida à mola não foi representada porque é interna ao sistema.
Passo 2
Então, aplicamos a Segunda Lei de Newton ao centro de massa, que é o mesmo centro da mola:
Resposta
Exercícios de Livros Relacionados
A bagagem no piso de um vagão-bagageiro de um trem de alta velocidade não está impedida de se movimentar, exceto pelo atrito. Determine o menor valor admissível do coeficiente de atrito estático entre
Um veleiro de 500 kg com seus tripulantes veleja a favor do vento a 12 km/h quando sua vela-balão é içada para aumentar a velocidade do veleiro. Determine a força resultante fornecida pela vela durant
Um trem leve composto de dois vagões viaja a 70 km/h. A massa do vagão A é 18.000 kg e a massa do vagão B é 13.000 kg. Quando os freios são acionados repentinamente, uma força de frenagem constante de
Uma bola de 125g que se move a uma velocidade de 3m / s atinge uma placa de 250g sustentada por molas. Admitindo que não haja perda de energia no impacto, determine ( a ) a velocidade da bola imediata
Um jogador de beisebol, ao pegar uma bola, pode amortecer o impacto levando sua mão para trás. Considerando que uma bola de 140g atinge sua luva a 140k m / h e que o jogador puxa sua mão para trás dur