Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 126
A bagagem no piso de um vagão-bagageiro de um trem de alta velocidade não está impedida de se movimentar, exceto pelo atrito. Determine o menor valor admissível do coeficiente de atrito estático entre uma caixa e o piso do vagão para que a caixa não deslize quando o trem diminuir sua velocidade a uma taxa constante de 200 km/h para 90 km/h em um intervalo de tempo de 12 s.
Passo 1
Então vamos resolver mais um exercício legal de dinâmica. Para determinar o coeficiente de atrito estático entre a caixa e o piso do vagão vamos utilizar o princípio do impulso e de quantidade de movimento linear. Primero, vamos ver como é o diagrama de corpo livre para esse problema:
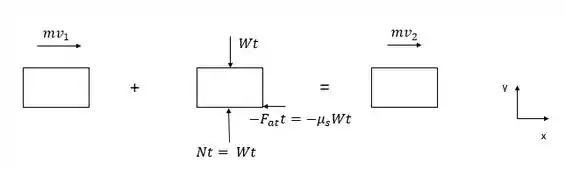
O impulso ocasionado pela força de atrito estático deve ser de forma que a caixa não deslize durante o intervalo de tempo de desaceleração. Assim, esse impulso é contrário ao movimento do trem. Somado os vetores em x temos:
Passo 2
Antes de substituir os valores na equação apresentada no passo 1, vamos converter as velocidades de km/h para m/s
A massa do vagão pode ser expressa como:
Substituindo na equação do passo 1 temos:
O coeficiente de atrito estático deve ser igual a 0,260