Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 120
Duas polias de de diâmetro estão montadas no eixo . As correias e ficam em planos verticais paralelos ao plano . Substitua as forças das correias mostradas por um sistema força-binário equivalente em .
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Queremos substituir as forças por um sistema força-binário em . Vamos trabalhar cada polia separadamente.
Para a polia com a correia , temos:
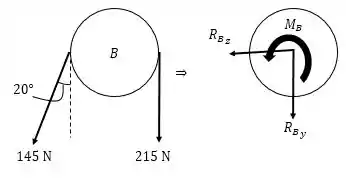
Onde:
E:
Portanto:
O momento resultante é dado por:
Passo 2
Para a polia com a correia , temos:
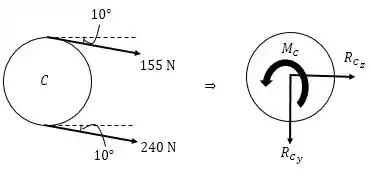
Onde:
E:
Portanto:
O momento resultante é dado por:
Passo 3
A resultante das forças é facilmente calculada como:
Para o cálculo do momento resultante em , precisamos calcular os vetores deslocamentos. Para cada ponto em que exista uma força aplicada, existirá um vetor deslocamento com origem em e fim no ponto de aplicação, logo:
Passo 4
Agora, podemos calcular o momento resultante em , através do produto vetorial do vetor deslocamento e das forças. Temos que:
Substituindo os valores, temos:
Resolvendo, temos que: