Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas - Ex. 81
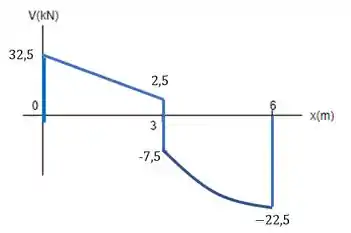
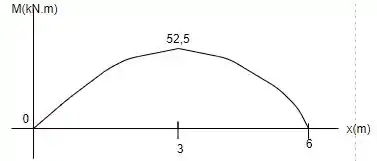
Determine os diagramas de esforço cortante e de momento fletor para a viga.
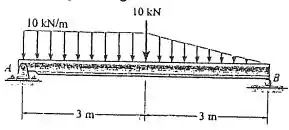
Passo 1
Fala, querido! Queremos os diagramas de esforços internos para essa viga aí!
Para determinar os diagramas de esforço, em primeiro lugar as reações de apoio devem ser determinadas.
Há algumas formas de fazer os diagramas depois desse passo. Uma delas é achando as equações desses esforços. A outra é utilizado métodos gráficos. Como o capítulo dessa questão trata de métodos gráficos, é isso que a gente vai usar, ok?
Uma observação antes de começar. Vamos lembrar duas coisas:
- se a derivada de uma função é positiva, nesse intervalo a função cresce, caso contrário, descresce.
- se a derivada segunda de uma função for positiva, a concavidade dela é para cima, caso contrário para baixo.
Agora sim, bora!
Passo 2
Vamos começar achando as reações:
Deve-se lembrar que a força resultante gerada por um carregamento triangular é dada por
E a posição do centroide é
Sendo que essa posição é em relação ao ponto incial do carregamento.
Enquanto que para um carregamento retangular tem-se
Deve-se analisar o DCL de toda a viga para encontrar as reações de apoio. Logo, tem-se:
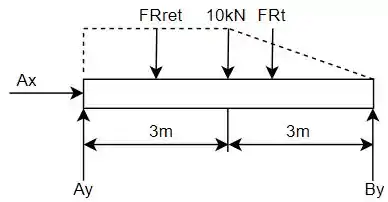
Como não há forças no eixo horizontal, a reação é nula.
Com o princípio dos momentos em relação ao ponto e tendo o sentido anti-horário como positivo:
Sendo assim, aplicando o equilíbrio de forças para o eixo :
Passo 3
Vamos começar fazendo o diagrama do cortante pelo método gráfico. Basicamente o que a gente faz nele é seguir setinhas (os sentidos e magnitude das forças).
Em temos a reação para cima, que vale . Então a gente sobe esse valor.
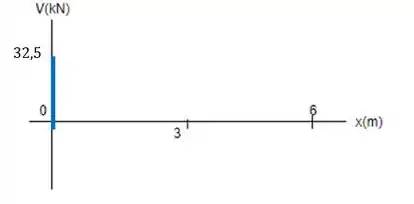
E nesse ponto já começa a carga distruibuida de .
Aí a gente faz uma reta descendo com inclinação de (a partir do ponto onde paramos em , depois de subir por causa de ) até chegar no ponto , onde o carregamento distrubuído acaba. Você pode reparar que descemos o valor da resultante do carregamento, mas como uma reta inclinada.
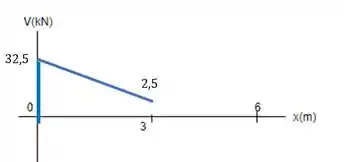
Depois, encontramos outra carga concetrada, a de para baixo. O que faz? Pula para baixo de onde a gente estava.
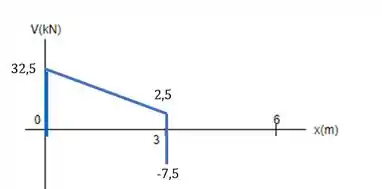
Passo 4
Aí cara, a gente acha um carregamento distribuído em forma de triângulo. Como a gente lida com esse cara? A gente vai pensar naquelas relações de derivada entre o carregamento e e suas implicações.
Como nosso carregamento é uma função linear, o cortante precisa ser uma função de um grau a mais, porque
Então o cortante precisa ser uma função de segundo grau. Com qual concavidade? Cara, essa relação acima vale para carregamentos positivos, no nosso caso, onde o carregamento está para baixo, temos:
O que nos diz se no intervalo, o carregamento for crescente (, a concavidade é para baixo, caso contrário, é para cima. No nosso triângulo, temos o segundio caso, então a concavidade é para cima.
No gráfico, a gente vai descer (no sentido das setinhas do carregamento) o valor da resultante desse primeiro triângulo, na forma de uma parábola com concavidade para cima, a partir do ponto que a gente estava até . Fica assim:
E no gráfico:
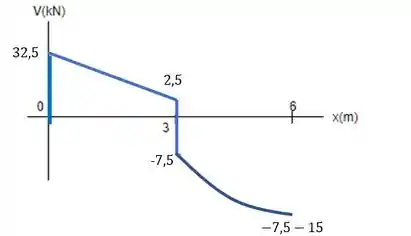
Depois disso, encontramos outra força concentrada, , então a gente pula para cima esse valor.
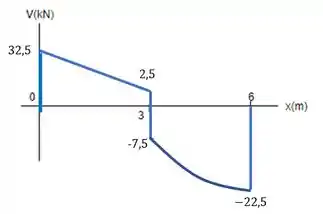
Prontinho! Se no final a gente chega em de novo, é porque estamos certinhos!
Passo 5
Agora para o diagrama de momento, a gente calcula os valores dos momentos nos pontos críticos, que no nosso caso, são os apoios, as extremidades e onde há mudança de carregamento.
Para , e para , , porque são apoios na extremidades e sem momentos concentrados.
A mudança de carregamento ocorre em . Então a gente calcula o momento nesse ponto, que vamos chamar de .
Imagina que a gente cortou nossa viga no meio, olhou para a esquerda e posiocionou na seção no sentido anti-horário (conveção positiva para o esforço interno olhando para a esquerda).
Depois disso, a gente acha o momento máximo. Isso ocorre em . Pelo gráfico do cortante, isso vai acontecer em . Já calculamos. Vamos seguir!
E sabendo que
Vemos que o momento deve ter um grau a mais que o cortante. Percebemos que o momento vai ser um polinômio do segundo grau de a (onde o cortante é uma reta inclinada, ou seja, uma função linear) e um polinômio de grau 3 de a , onde o cortante é um parábola.
E como
Se o cortante for descrescente, a concavidade do momento é para baixo. E isso é exatamente o que acontece no nosso caso de a .
Então o momento vai ser um polinômio de segundo grau até , e depois de terceiro grau. E todo o gráfico terá concavidade para baixo, extremos em zero e máximo em . Assim:
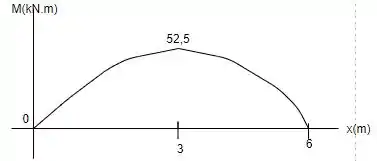
Resposta
