Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 131b

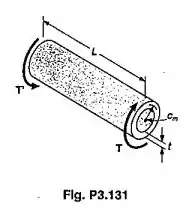
Um eixo cilíndrico vazado de comprimento L, raio médio c m e espessura uniforme t , está submetido aos torques de intensidade T .   Considerar inicialmente os valores da tensão média de cisalhamento τ m e d e o ângulo de torção ϕ obtido das fórmulas de torção elástica desenvolvidas nas Secs 3.4 e 3.5, e também os correspondentes valores obtidos das fórmulas desenvolvidas na Sec 3.13, para eixos vazados de paredes finas. Pede-se (a) mostrar que o erro relativo, introduzido em usar as fórmulas de eixo de parede fina, ao invés das fórmulas de torção elástica é o mesmo para τ m e d e ϕ ,   e que este erro relativo é positivo e proporcional ao quadrado da relação t / c m (b) calcular o erro percentual correspondente a valores de t / c m iguais a 0,1 , 0,2 e 0,4 .

Passo 1

No item A) a gente calculou a seguinte equação.

τ τ m e d = 1 + t 2 c m 2

Então o erro será

e r r o = t 2 c m 2

Para t c m = 0,1

e r r o = t 2 c m 2

e r r o = 1 2 ⋅ 0,1 2

e r r o = 0,0025

e r r o = 0,25 %

Passo 2

Para t c m = 0,2

e r r o = t 2 c m 2

e r r o = 1 2 ⋅ 0,2 2

e r r o = 0,01

e r r o = 1 %

Passo 3

Para t c m = 0,4

e r r o = t 2 c m 2

e r r o = 1 2 ⋅ 0,2 2

e r r o = 0,04

e r r o = 4 %

Resposta

e r r o = 0,25 %

e r r o = 1 %

e r r o = 4 %

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O eixo sólido mostrado é de um aço doce o qual se considera elastoplástico com G=77GPa e τ=145MPa. Determinar o ângulo de torção causado pela aplicação de um torque T1 = 600N.m e T2 = 1000 N.m.
O eixo maciço mostrado é de um aço doce o qual se considera elastoplástico com G=77GPa e τ=145MPa. Determinar a máxima tensão de cisalhamento e o raio do núcleo elástico, devido à aplicação de um torq
Um eixo vazado mostrado é feito de um aço doce, o qual se considera ser elastoplástico com G = 77 GPa e τ=145MPa. Determinar o ângulo de torção quando o eixo se torna totalmente plástico.
Um eixo maciço de 0,9 m tem um diâmetro de 63,5 mm e é feito de um aço doce o qual se considera ser elastoplástico com G = 77 GPa e τ=145MPa. Determinar o torque necessário para torcer o eixo, de um â
O eixo escalonado mostrado deve transmitir 120 kW a uma velocidade de 480 rpm. Sabendo-se que a tensão de cisalhamento admissível no eixo é de 55MPa, determinar o menor raio r permissível para o adoça