Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 128
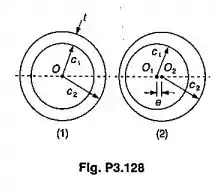
Um eixo cilíndrico vazado foi projetado com a seção transversal mostrada na Fig (1) para resistir a um torque máximo . Um defeito na fabricação, no entanto, resultou em uma pequena excentricidade e, entre as superfícies cilíndricas, interna e externa, como mostrado na FIg. (2). Pede-se
- Expressar o torque máximo que pode ser aplicado com segurança ao eixo defeituoso, em termos de e .
- Calcular o decréscimo percentual do torque admissível para valores da relação , iguais a e
Passo 1
A chave da questão é a gente perceber que nas duas situações a área é a mesma.
Para calcular a área interna vamos considerar a o raio médio entre e :
Passo 2
Inicialmente vamos considerar o eixo (1).
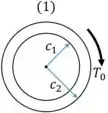
A espessura do eixo (1) é:
Podemos calcular a tensão no eixo (1):
Passo 3
Agora vamos pensar no eixo (2).
Como a espessura varia, então a tensão no eixo (2) vai variar.
Se a gente olhar para a fórmula dá para perceber que quanto menor o valor de maior vai ser a tensão.
Com isso em mente, vamos calcular a maior tensão possível no eixo (2).
A menor espessura no eixo (2) é:
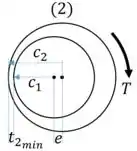
E agora aplicamos na equação da tensão em paredes finas:
Passo 4
O maior torque permitido no eixo (2) acontece quando é igual a
Isolamos
Fazemos as simplificações:
E chegamos no valor de