Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 45
O eixo maciço de aço mostrado está submetido aos torques de , aplicados nas extremidades e . Usando , determinar a energia de deformação do eixo.
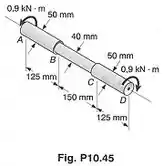
Passo 1
Oi, galera! Como está a vida? Vamos fazer uma questão de energia de deformação pra alegrar?
Nesse exercício precisamos calcular a energia de deformação da barra que tem diâmetro variável. Pra calcular a energia de deformação dessa barra grande , precisamos dividí-la em barras com diâmetros iguais! No nosso caso, dividiremos a barra em três barras: a barra de energia , a barra de energia e a barra de energia .
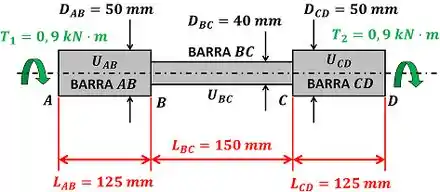
, e são os diâmetros das barras , e respectivamente. , e são os comprimentos das barras , e respectivamente. e são os torques que torcem a barra .
Como a barra é a soma das barras , e , a energia da barra é a soma das energias de deformação , e das barras , e .
Para calcular as energias de deformação , e das barras , e com áreas de seção transversal constantes e torques constantes, precisamos usar a equação 10.22 do livro que serve para esse caso barras com áreas constantes e torques constantes.
é o módulo de elasticidade transversal do material da barra. Ele vale segundo o enunciado. , e são os torques que agem nas barras , e respectivamente.
Agora que temos todas essas fórmulas, vamos começar a fazer as contas, calculando , e !
Passo 2
Vamos calcular quanto valem os torques das barras , e . Achamos esses valores, usando a equação de equilíbrio de momento em cada barra. Essa equação diz que a soma de todos os torques em cada barra deve ser igual a zero. Ou seja, se um torque gira a barra para um lado, deve haver um torque igual que faça a barra girar pro outro lado!
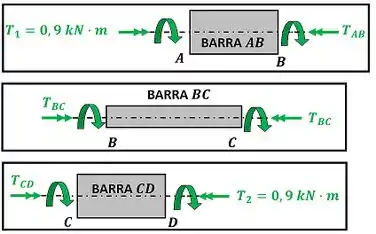
Na figura acima, nós vemos os torques que são aplicados em cada barra.
No entanto, para resolver o problema, precisamos lembrar da lei da ação e reação.
Quando a barra aplica um torque na barra , a barra reage com um torque igual de sentido contrário! Isso significa que (o torque que a barra faz em ) tem que ser igual a (o torque que a barra faz em ).
Isso não para por aí. As barras e estão conectadas. Isso significa que o torque que a barra aplica na barra deve ser igual ao torque que a barra aplica na barra por causa da lei de ação e reação.
Isso quer dizer que só precisamos achar quando vale !
Calculamos , dizendo que a soma desses torques vale zero, porque a barra está parada.
A figura abaixo mostra os torques aplicados na barra
Como o torque faz a barra girar para o sentido contrário (setinha verde do torque está pra esquerda), colocamos um sinal de menos na frente desse torque.
Logo:
Com esses valores de torque, falta apenas calcular os valores dos momentos de inércia polares , e de cada barra para achar , e .
Passo 3
Antes de achar as energias de deformação , e de cada barra, temos que encontrar os valores dos momentos de inércia polares , e de cada barra
Fazemos isso, através das fórmulas de momentos de inércia polares para áreas circulares abaixo. Antes, devemos converter os diâmetros de pra , multiplicando eles por .
Com , e , já podemos calcular as energias de deformação de cada barra no próximo passo!
Passo 4
Substituímos , e nas equações de , e para achar as energias de deformação. No entanto, antes disso nós precisamos converter os comprimentos de pra (multiplicando eles por ) e converter o de para (multiplicando ele por ).
Somando essas três energias de deformação, conseguimos achar a energia de deformação total que a questão pede!