Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 50
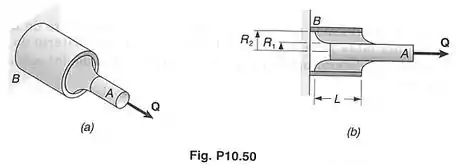
Um cilindro vazado de borracha liga uma barra , de raio , a um tubo , de raio interno , formando um suporte isolante de vibração. Denotando por o módulo de elasticidade transversal da borracha, determinar a energia de deformação do cilindro vazado de borracha para o carregamento mostrado.
Passo 1
E aí, meus queridos! Como vocês estão?
Esse é um bom exercício de energia de deformação que te ajudar a se preparar pra sua prova!
A questão pede que a gente calcule a energia de deformação de um cilindro vazado de borracha que liga a barra a um tubo . Como veremos no diagrama de corpo livre da borracha, ele só está submetido a forças de cisalhamento. Isso significa que ele possui apenas deformações de cisalhamento e sua energia pode ser calculada pela equação 10.20 do livro.
onde é a tensão de cisalhamento da borracha, é o módulo de elasticidade transversal da borracha, é o volume da borracha e é o volume de um elemento infinetesimal da borracha.
Esses termos são mostrados na figura abaixo.
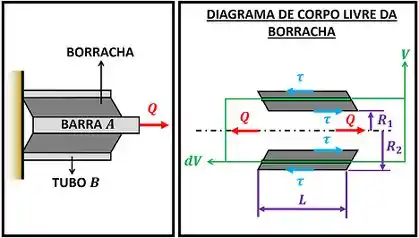
é a distância entre o eixo da borracha e um ponto qualquer da borracha.
Por essa figura, nós vemos que a barra aplica na borracha uma força cisalhante para a direita. Além disso, o tubo aplica na borracha uma força cisalhante para a esquerda. Essas duas forças cisalhantes são aplicadas no eixo da borracha cilíndrica.
Agora que entendemos tudo isso, podemos partir para o próximo passo!
Passo 2
Para conseguir resolver a integral de , precisamos saber quanto vale a tensão de cisalhamento da borracha.
Essa tensão é igual à força de cisalhamento dividida pela área cilíndrica sobre a qual a tensão é aplicada.
A figura abaixo mostra melhor quanto vale essa área .
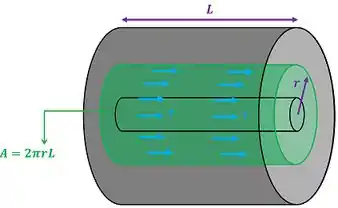
Substituindo o valor de presente na figura na equação de , achamos:
Agora sim somos capazes de tentar resolver a integral de !
Passo 3
Substituindo o valor de que deduzimos na equação de , encontramos:
No entanto, essa integral ainda está em função de . O volume de um elemento infinitesimal cilíndrico está presente na figura abaixo!
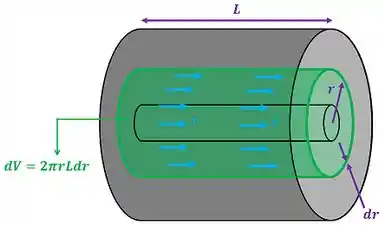
Podemos substituir essa nova informação na integral para tentar resolvê-la.
Vamos deixar para o passo seguinte a resolução dessa integral.
Passo 4
Primeiro, precisamos colocar as constantes para fora da integral.
Depois, encontramos a integral.
Substituindo os limites de integração:
Parabéns! Conseguir resolver mais uma questão!