Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 95

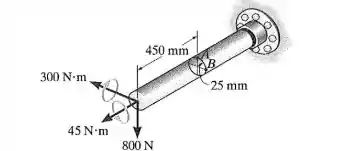
O eixo maciço está sujeito a torque, momento fletor e força de cisalhamento como mostra a figura. Determine as tensões principais que agem nos pontos A e B e a tensão de cisalhamento máxima absoluta.

Passo 1

Fala aí pessoal, vamos para mais um problema de resmat. Este problema é simples e direto, mas temos que ir com calma porque são dois pontos com os quais vamos trabalhar. Primeiro, vamos determinar os esforços atuantes:

V = 800 N

T = 45 N m

M = 800 × , 045 - 300 = 60 N m

Com isso, já podemos determinar as tensões cisalhantes e normais nos pontos A e B:

σ A = M y I = 4,889 M P a

τ A = 1,833 M P a

σ B = 0

τ B = - 1,29 M P a

Passo 2

O problema não nos pede essas tensões, mas sim as tensões principais. Com isso, podemos calcular estas por meio da fórmula:

σ 1,2 = σ x + σ y 2 ± σ x - σ y 2 2 + τ x y 2

Para o ponto A, teremos:

σ 1 = 5,5 M P a

σ 2 = - 0,611 M P a

Logo:

σ M á x = 5,5 M P a

σ i n t = 0

σ m í n = - 0,611 M P a

Já a tensão cisalhante máxima absoluta será:

γ m á x   a b s = σ m á x - σ m í n 2 = 3,06 M P a

Para o ponto B, teremos:

σ 1 = 1,29 M P a

σ 2 = - 0,611 M P a

Logo:

σ M á x = 1,29 M P a

σ i n t = 0

σ m í n = - 1,29 M P a

Já a tensão cisalhante máxima absoluta será:

γ m á x   a b s = σ m á x - σ m í n 2 = 1,29 M P a

Resposta

Para o ponto A:

σ M á x = 5,5 M P a

σ i n t = 0

σ m í n = - 0,611 M P a

γ m á x   a b s = 3,06 M P a

Para o ponto B:

σ M á x = 1,29 M P a

σ i n t = 0

σ m í n = - 1,29 M P a

γ m á x   a b s = 1,29 M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A tensão em um ponto é mostrada no elemento. Determine as tensões principais e a tensão de cisalhamento máxima absoluta.
Desenhe os três círculos de Mohr que descrevem cada um dos seguintes estados de tensão.
Desenhe os três círculos de Mohr que descrevem cada um dos seguintes estados de tensão.
O parafuso está preso a seu suporte em C. Se a força de 90 N for aplicada à chave para apertá-lo, determine as tensões principais e a tensão de cisalhamento máxima absoluta desenvolvidas na haste do p