Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 90
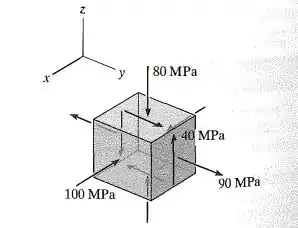
A tensão em um ponto é mostrada no elemento. Determine as tensões principais e a tensão de cisalhamento máxima absoluta.
Passo 1
Fala galera, bora para mais um exercício de resmat. Esse tipo de questão tem um passo a passo bem definido. Bora seguir!
Primeriro, a gente identifica o plano que não tem tensões cisalhantes. É o plano , certo? O interessante, é que a gente pode dizer de cara que a tensão normal nele é uma tensão principal! Maneiro, né?
Achamos então nossa primeira tensão principal
E e aí, para achar as outras tensões principais, nosso problema vira um estado plano de tensões. Com essa carinha:
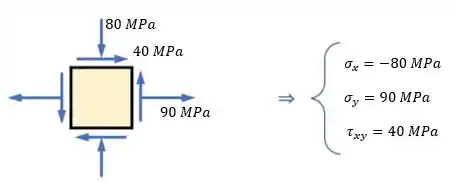
Vamos resolver esse problema que surgiu!
Passo 2
Vamos resolver ele pelo círculo de Mohr.
Temos que determinar o centro do círculo, definido como:
O segundo ponto que vamos determinar representa as tensões no eixo do seu estado de tensões e é definido como:
Tendo estes dois pontos, podemos liga-los e assim temos o raio do círculo. Seu esboço vai ser assim:
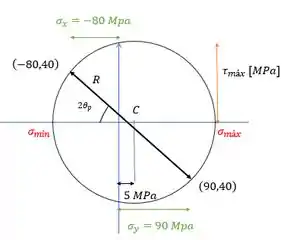
Repara que a gente també colocou ai o ponto que representa a tensão em , de coordenada .
Passo 3
Para determinarmos as tensões principais usando o círculo de Mohr, precisamos calcular o raio do círculo. Temos:
Com isso, podemos calular as nossas tensões principais e , dadas por:
Substituindo, temos:
Passo 4
Agora a gente tem as 3 tensões principais do nosso estado triaxial:
Aí a gente pode colocar o nome delas certinho, comparando os valores dessas tesões entre si.
A tensão máxima é:
E para a tensão mínima, temos:
Para a tensão, intermediária, temos:
Passo 5
Por fim, podemos determinar a tensão de cisalhamento máxima absoluta a partir da fórmula: