Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 113

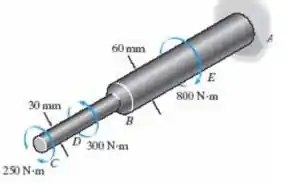
O eixo está preso à parede em A e é submetido aos torques mostrados na figura. Determine a tensão de cisalhamento máxima no eixo. Um filete de solda de raio 4,5   m m é usado para interligar os eixos em B.

Passo 1

Dados do problema: D = 60   m m ,   d = 30   m m ,   r = 4,5   m m

A chave para resolver o problema é que precisamos calcular a tensão em mais de um ponto de interesse.

Fora isso, a questão se desenvolve sem dificuldades: calculamos o coeficiente de contração de tensão, calculamos o momento de inércia polar e aplicamos tudo isso na fórmula da tensão.

Passo 2

Vamos calcular as reações de apoio. Como o carregamento são apenas torques, a reação de apoio também será apenas um torque:

∑ T = 0 - 250 + 300 - 800 + T A = 0 T A = 750   N m

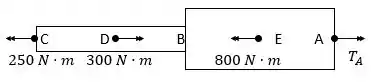
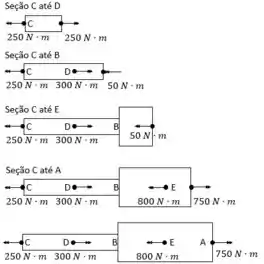
Em posse das reações de apoio podemos analisar os esforços internos. Analisando as diversas seções feitas encontramos três pontos de interesse: O ponto A onda o torque é máximo, o ponto B onde há concentração de tensão, e o segmento CD onde ocorre o maior torque no segmento mais fino do eixo.

T m a x = T A = 850   N m T B = 50   N m T C D = 250

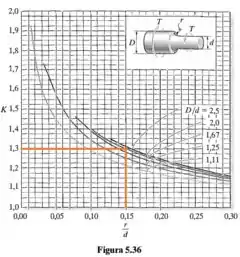
Passo 3

Calculado o coeficiente de concentração de tensão:

D d = 60 30 = 2 r d = 4,5 30 = 0.15

K = 1,3

Passo 4

Vamos calcular o momento de inércia nos nossos pontos de interesse, lembrando que as características geométricas do ponto B e do segmento CD são as mesmas.

J A = π D 4 32 = π   ⋅ 60 4 32 ⇒ J A = 1272345,024   m m 4

J B = π d 4 32 = π   ⋅ 30 4 32 ⇒ J B = 79521,564   m m 4 Os raios em cada ponto:

c A = D 2 = 60 2 ⇒ c A = 30   m m c B = d 2 = 30 2 ⇒ c B = 15   m m  

Passo 5

Para concluir, calculamos as tensões em cada ponto.

Ponto B:

τ B = T B c B J B K = 50 ⋅ 15 79521,564 ⋅ 1,3 ⋅ N m ⋅ m m m m 4 ⇒ τ B = 12,26   M P a

Ponto A:

τ A = T c J = 750 ⋅ 30 1272345 , 024 ⋅ N m ⋅ m m m m 4 ⇒ τ A = 17,68   M P a

Ponto CD:

τ C D = T C D c B J B = 250 ⋅ 15 79521,564 ⋅ N m ⋅ m m m m 4 ⇒ τ C D = 47,16   M P a

Resposta

A maior tensão que atua no eixo é:

τ C D = 47,16   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um eixo vazado mostrado é feito de um aço doce, o qual se considera ser elastoplástico com G = 77 GPa e τ=145MPa. Determinar a intensidade do torque T e o correspondente ângulo de torção para quando i
O eixo sólido mostrado é de um aço doce o qual se considera elastoplástico com G=77GPa e τ=145MPa. Determinar a intensidade do torque T necessário para torcer o eixo, de um ângulo de 15°.
O eixo escalonado mostrado deve transmitir 150kW. Sabendo-se que a tensão de cisalhamento admissível no eixo é de 55MPa e que o raio de adoçamento é r = 6mm, determinar a menor frequência possível.
Um eixo vazado mostrado é feito de um aço doce, o qual se considera ser elastoplástico com G = 77 GPa e τ=145MPa. Determinar a intensidade do torque T e o correspondente ângulo de torção para quando a
O eixo sólido mostrado é de um aço doce o qual se considera elastoplástico com G=77GPa e τ=145MPa. Determinar o raio do correspondente núcleo elástico.