Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 111

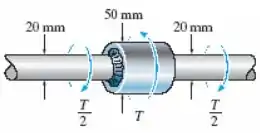
A tensão de cisalhamento admissível para o aço usado no eixo é τ a d m = 8   M P a . Se os lementos forem interligados por um filete de solda de raio r = 4   m m , determine o torque máximo T que pode ser aplicado.

Passo 1

Vamos separar os dados fornecidos pela questão:

τ a d m = 8   M P a r = 4   m m D = 50   m m d = 20   m m

O nosso objetivo nessa questão é simplemente aplicar a equação 5.21 para descobrir o valor do torque que pode ser aplicado.

Para isso vamos precisar analisar a concentração de tensão na estrutura, o momento de inércia e a distribuição dos torques internos.

Passo 2

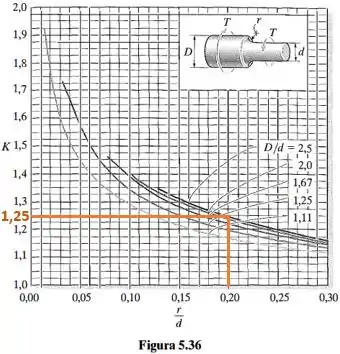
Vamos calcular o fator de concentração de tensão de acordo com o gráfico da Figura 5.36.

Primeira calculamos a relação entre os diâmetros:

D d = 50 20 = 2.5

E depois calculamos a relação entre o diâmetro menor e o raio do filete

r d = 4 20 = 0.2

E podemos colocar estes dados na figura e descobir o valor do coeficiente de concentração de tensão.

K = 1.25

Passo 3

Agora vamos calcular as definições geométricas da estrutura

Momento de Inércia:

J = π   ⋅ d 4 32 J = π ⋅ 20 4 32 J = 5000 π   m m 4

E o raio de torção:

c = d 2 c = 10   m m

Passo 4

Se fizermos sucessivas seções na figura, vamos encontrar a seguinte distribuição de esforços internos:

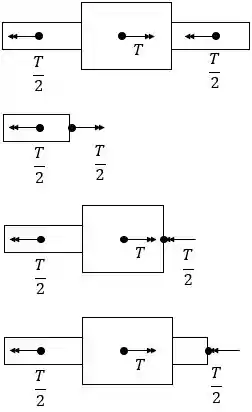
Observe que em todas as seções, o maior torque interno possível é

T m á x = T 2

Passo 5

Agora aplicamos a equação do torque com concentração de tensão:

τ a d m = T m á x ⋅ c J K τ a d m = T 2 ⋅ c J K T = 2 ⋅ τ a d m ⋅ J K ⋅ c T = 8 ⋅ 5000 π 1.25 ⋅ 10 ⋅ M P a ⋅ m m 4 m m T = 20.1   N m

Resposta

T = 20.1   N m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o torque necessário para torcer um cabo de aço curto de 3 m m de diâmetro por várias revoluções se ele for feito de um aço que se presume ser elástico-plástico com tensão de escoamento τ e =
Um eixo maciço tem diâmetro de 40 m m e comprimento de 1 m e é feito de um material elástico-plástico com tensão de escoamento τ e = 100 M P a . Determine o torque elástico máximo T e e o ângulo de to
Um eixo maciço com diâmetro de 50 m m é feito de material elástico-plástico com tensão de escoamento τ e = 112M P a e módulo de cisalhamento G = 84G P a . Determine o torque exigido para desenvolver u
O eixo é submetido a um torque T que produz escoamento na superfície do segmento de maior diâmetro. Determine o raio do núcleo elástico produzido no segmento de menor diâmetro. Despreze a concentração
O eixo é composto por duas seções rigidamente acopladas. Se o material for elástico perfeitamente plástico como mostra a figura, determine o maior torque T que pode ser aplicado eixo. Além disso, dese