Foi assumido na SEC.4.4 , que as tensões normais em um membro em flexão pura são desprezadas. Para um membro elástico, de seção transversal retangular, inicialmente reto, pede-se:
- Derivar uma expressão aproximada para , como uma função de y;
- Mostrar que e, então, que pode ser desprezado em todas as situações práticas.
[Sugestão: Considerar o diagrama de corpo livre da porção da viga localizada abaixo da superfície de ordenada y e assumir que a distribuição de tensões é sempre linear.]
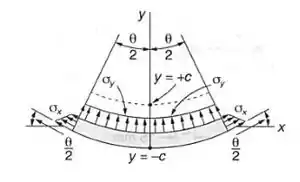
Passo 1
Começando com o cálculo do comprimento da região encurvada, podemos definir que a mesma será dada por:
Com isso temos que o ângulo da região encurvada é dado por:
Supondo a espessura da chapa como sendo , podemos fazer o somatório de forças na direção y, com isso teremos que:
- Força na direção Y devido a tensão em y
Supondo o comprimento da barra como e largura da barra como sendo , podemos analisar cada estrutura da seguinte maneira.
E como a tensão x sofre uma variação, precisamos usar uma integração, que vária do ponto mais baixo da estrutura até .
E ainda temos que lembrar de decompor a tensão em x:
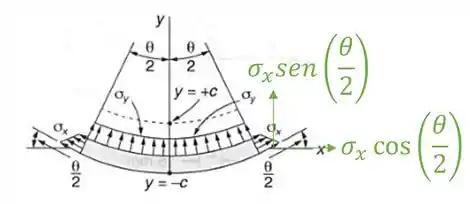
Com isso teríamos que:
E temos que tomar cuidado, poie temos tensão em x no lado esquerdo e no lado direito, ou seja, essas duas tensões geraram duas forças, com isso teremos que:
E para podermos pegar a variação entre , precisamos de uma integral.
E como o ângulo é pequeno, podemos definir a seguinte aproximação:
Com isso teremos que:
E sabemos que:
Substituindo teremos que:
Uma relação importante que precisamos saber, é uma relação entre a tensão máxima na direção x e a tensão atuante, que é dada por:
E porque fazemos isso? Porque a nossa integral está em função de y,e com isso passamos a ter uma tensão em função de y também, substituindo teremos que:
Resolvendo a integral teremos que:
E assim resolvemos o nosso item A) calculando uma tensão em y em função da direção y.
Passo 2
No item B) queremos o máximo valor da tensão em y, e para termos a máxima tensão na direção y, precisamos ter que:
Substituindo na nossa equação teremos que:
Resposta
- Item a)
- Item b)