Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 32

Um perfil laminado de aço W 410 x 114   está sujeito a um momento M de 360   k N m . Sabendo-se que E = 200   G P a e ϑ = 0,30 , determinar:

  1. A variação da largura da aba superior;
  2. A variação do comprimento da metade superior AC da alma do perfil.

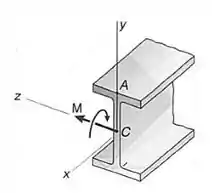
Passo 1

Sabemos que o raio de curvatura longitudinal da nossa barra pode ser escrita da seguinte maneira:

1 ρ = M E I

Sabemos que:

ρ = E I M

e se quisermos determinar as deformações, teremos que fazer o seguinte

ε t = ϑ ε l

Sabemos que:

ε t = c ρ '

ε l = c ρ

Loco teremos que:

ε t = ϑ c ρ     e   ε z = ϑ c ρ  

Passo 2

Agora que temos a LN, podemos determinar o momento de inércia, e com isso vamos seguir o seguinte passo a passo.

  • I

    • I = 462   .   10 6   m m 4

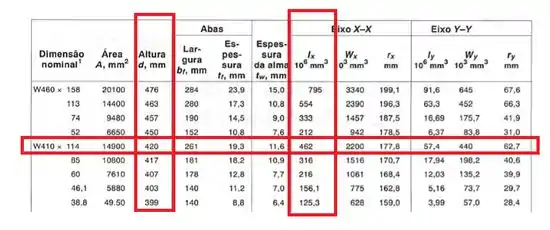
    E também temos que:

    c = 420 2 = 210   m m

    Passo 3

    Se resolvermos o item b primeiro será mais fácil.

  • Item b)

    • ρ = E I M

    Sabemos pelo enunciado que:

    I = 462   .   10 6 m m 4

    E = 200   G P a = 200000   M P a = 200000 N m m 2

    M = 360   k N m = 360000   N m = 360000000   N m m

    Substituindo teremos que:

    ρ = 200000 N m m 2   .   462   .   10 6   m m 4   360000000   N m m = 256667   m m = 257   m

    E para termos a deformação longitudinal teremos que:

    ε z = ϑ c ρ = 0,30 210   m m 256667   m m = 2,45   .   10 - 4

    E sabemos que:

    ε z = ∆ a c A C = 2,45   .   10 - 4

    ∆ a c = 210   .   2,45   .   10 - 4 = 0,051   m m

  • Item a)

    • ε t = ϑ c ρ = 0,3   .   210   256667   = 2,45   .   10 - 4

    Sabemos que:

    ε t = ∆ b f b f = 2,45   .   10 - 4

    ∆ b f = 261   .   2,45   .   10 - 4 = 0,064   m m

    Resposta

  • Item a)

    • ∆ b f = 0,064   m m

  • Item b)

∆ c = 0,051     m m

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se o eixo tiver um diâmetro de 40m m , determine a tensão de flexão máxima absoluta no eixo.
Se a lança do guindaste A B C tiver seção transversal retangular com base 50m m e altura de 75m m , determine a tensão de flexão máxima absoluta na lança.
Se o tubo tiver diâmetro externo de 30m m e espessura de 10m m , determine a tensão de flexão máxima absoluta no eixo.
Se o eixo tiver um diâmetro de 50m m , determine a tensão de flexão máxima absoluta no eixo.
Se a viga ACB tiver seção transversal quadrada de 150m m por 150m m , determine a tensão de flexão máxima absoluta na viga.