Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 119
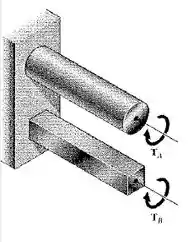
O eixos A e B são feitos do mesmo material e têm o mesmo comprimento e a mesma área de seção transversal, mas A tem uma seção transversal circular e B tem uma seção transversal quadrada. Determine a relação entre os ângulos pelos quais os eixos A e B, respectivamente, podem suportar quando estão sujeitos ao mesmo torque (). Assumir que ambas as deformações sejam elásticas.
Passo 1
Bom, pra resolver essa questão, vamos começar chamando c do raio da seção circular da barra A, e vamos chamar de b a medida do lado da seção quadrada da segunda barra, tranquilo?
Para que ambos tenham a mesma área teremos que
Isolando b então
Passo 2
Para o cículo temos a relação
Temos ainda que
Onde
Aplicando na fórmula teremos
Como o enunciado quer a relação entre os ângulos, vamos isolar esse da primeira equação que usamos e substituir esse que descobrimos. Temos então
Para a base quadrada temos da teoria que
, logo
Temos ainda para o
Passo 3
Bom, para descobrirmos então a relação entre faremos essa divisão
Quando
Como teremos então
perfeitinho!