Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 11

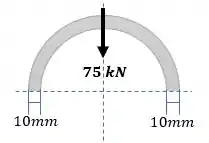
Se o tubo estiver sujeito a um cisalhamento V = 75   k N , determine a tensão de cisalhamento máxima nele.

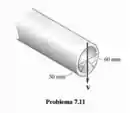
Passo 1

Dados da questão: V = 75   k N ,   r = 50 m m ,   R = 60 m m ,   t = 10 m m

A questão pede: A tensão máxima τ m á x = ?

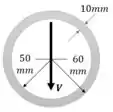
A questão é bem direta, basta a gente calcular a tensão máxima pela Equação 7.3. Antes precisamos calcular o Momento de Inércia e o Momento Estático.

Passo 2

Começamos calculando o momento de inércia. Para isso basta subtrair o momento de inércia do diâmetro maior pelo menor:

I = π R 4 4 - π r 4 4

I = π ⋅ 60 4 4 - π ⋅ 50 4 4

I = 5,27 ⋅ 10 6 m m 4

Passo 3

Agora vamos calcular o momento estático. Observe a figura abaixo, perceba que o momento estático que nos interessa pode ser obtido pela subtração do momento estático laranja pelo amarelo. Pra fazer esse cálculo, lembre-se que o centroide de um semicírculo é:

y s e m i   c í r c u l o = 4 R 3 π

Q = Q L a r a n j a - Q A m a r e l o

Q = A L a r a n j a ⋅ y L a r a n j a - A A m a r e l o ⋅ y A m a r e l o

Q = 1 2 π R 2 ⋅ 4 R 3 π - 1 2 π r 2 ⋅ 4 r 3 π

Q = 2 3 ( R 3 - r 3 )

Q = 2 3 ( 60 3 - 50 3 )

Q = 60667   m m 3

Passo 4

Agora só aplicar a Equação 7.3. Observe que na região a espessura onde o cisalhamento atua é igual a duas vezes a espessura.

τ = V Q I ⋅ 2 t

τ = 75 k N ⋅ 60667   m m 3 5,27 ⋅ 10 6 m m 4 ⋅ 2 ⋅ 10 m m

τ = 43,17 × 10 6   N / m 2

τ = 43,17   M P a

Resposta

τ = 43,17   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga em balanço mostrada consiste em um perfil em forma de “Z”, de espessura uniforme. Para o carregamento mostrado, determinar a distribuição de tensões de cisalhamento na perna vertical BD. Os eix
Duas pranchas de 50 x 150 mm de seção transversaç são conectadas através de parafusos de fenda, para formar uma viga que é submetida a uma força vertical de 1800 N. Sabendo-se que a força de cisalhame
Para uma viga de madeira com a seção transversal mostrada, determinar a maior força cortante vertical admissível, se a tensão de cisalhamento não deve exceder a 1035k P a . Considere w = 50m m .
Duas placas retangulares são soldadas a um perfil de aço laminado com abas largas, formando a viga mostrada. Determinar a maior força cortante admissível, se a tensão de cisalhamento na viga não deve
Para uma viga de madeira com a seção transversal mostrada, determinar a maior força cortante vertical admissível, se a tensão de cisalhamento não deve exceder a 1035k P a .